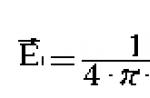თუ ელექტრული ველი იქმნება ერთი წერტილის მუხტით ქ, მაშინ ამ ველის სიძლიერე მანძილზე მდებარე ნებისმიერ წერტილში რგადასახადი თანაბარია, კულონის კანონის მიხედვით:
და მიმართულია მუხტის ამ წერტილთან დამაკავშირებელი სწორი ხაზის გასწვრივ. ამრიგად, წერტილის მუხტის ველის სიძლიერე იცვლება მუხტიდან დაშორებით მანძილის კვადრატის უკუპროპორციით. დადებითი მუხტით ქველი მიმართულია მუხტის რადიუსის გასწვრივ, უარყოფითით ქ– რადიუსის გასწვრივ მუხტისკენ. ვნახოთ, რას უდრის ორი წერტილის მუხტით გამოწვეული ველის სიძლიერე q 1და q 2. დაე E 1- ველის სიძლიერე რაღაც მომენტში აბრალდებით გამოწვეული q 1(დატენვისას q 2წაშლილია) და E 2– დაძაბულობა იმავე წერტილში, რომელიც გამოწვეულია დამუხტვით q 2(როდესაც ბრალდება მოიხსნება q 1). ეს მნიშვნელობები განისაზღვრება ფორმულებით:
გამოცდილება გვიჩვენებს, რომ ორივე მუხტის კომბინირებული მოქმედებით, ველის სიძლიერე წერტილში აშეგიძლიათ იპოვოთ პარალელოგრამის წესით:
თუ წერტილიდან ადაყარეთ სეგმენტები, რომლებიც ასახავს დაძაბულობის სიდიდეს და მიმართულებას E 1 და E 2 და ამ სეგმენტებზე, როგორ ავაშენოთ პარალელოგრამი გვერდებზე, შემდეგ დაძაბულობა ე მიღებული ველი სიდიდითა და მიმართულებით იქნება წარმოდგენილი ამ პარალელოგრამის დიაგონალით .
ველის სიძლიერის დამატების წესი მსგავსია მექანიკაში ძალების დამატების წესის. ისევე, როგორც მექანიკაში, პარალელოგრამის წესის გამოყენებადობა ნიშნავს ელექტრული ველების მოქმედების დამოუკიდებლობას. პარალელოგრამის წესის თანმიმდევრული გამოყენებით, შეგიძლიათ გამოთვალოთ ველის სიძლიერე მხოლოდ ორზე მეტი. მაგრამ ასევე ნებისმიერი რაოდენობის ქულების გადასახადი.
მუხტების სისტემის ველის სიძლიერე მოცემულ წერტილში უდრის ველის სიძლიერის გეომეტრიულ (ვექტორულ) ჯამს, რომელიც იქმნება ამ დროს თითოეული მუხტის მიერ ცალკე:
ამ განცხადებას ეწოდება ელექტროსტატიკური ველების სუპერპოზიციის პრინციპი.
საცნობარო ინფორმაცია:
დაძაბულობის ხაზები – ხაზები, რომელთა ტანგენტები ველის თითოეულ წერტილში ემთხვევა ამ წერტილში ელექტროსტატიკური ველის სიძლიერის ვექტორს.
დაძაბულობის ხაზები არ იკვეთება.
დადებითი მუხტი არის დაძაბულობის ხაზების წყარო; უარყოფითი მუხტი არის დაძაბულობის ხაზების გადინება.
ინტენსივობის ვექტორის სიდიდე პროპორციულია ელექტროსტატიკური ველის ინტენსივობის ხაზების კონდენსაციის ხარისხთან. ელექტრულ ველს, რომლის ინტენსივობის ვექტორები ერთნაირია სივრცის ყველა წერტილში, ეწოდება ერთგვაროვანი.
ეს არის დებულება, რომელიც გამოიყენება რიგ შემთხვევებში. ეს არის ერთ-ერთი ზოგადი ფიზიკური კანონი, რომელზედაც აგებულია ფიზიკა, როგორც მეცნიერება. ეს არის ის, რაც მას შესანიშნავს ხდის მეცნიერებისთვის, რომლებიც იყენებენ მას სხვადასხვა სიტუაციებში.
თუ განვიხილავთ სუპერპოზიციის პრინციპს ყველაზე ზოგადი გაგებით, მაშინ მისი მიხედვით, ნაწილაკზე მოქმედი გარე ძალების გავლენის ჯამი იქნება თითოეული მათგანის ინდივიდუალური მნიშვნელობების ჯამი.
ეს პრინციპი ვრცელდება სხვადასხვა წრფივ სისტემაზე, ე.ი. სისტემები, რომელთა ქცევა შეიძლება აღწერილი იყოს წრფივი ურთიერთობებით. მაგალითი იქნება მარტივი სიტუაცია, როდესაც წრფივი ტალღა ვრცელდება კონკრეტულ გარემოში, ამ შემთხვევაში მისი თვისებები შენარჩუნდება თვით ტალღისგან წარმოქმნილი დარღვევების გავლენის ქვეშაც კი. ეს თვისებები განისაზღვრება, როგორც თითოეული ჰარმონიული კომპონენტის ეფექტის სპეციფიკური ჯამი.
გამოყენების სფეროები
როგორც უკვე აღვნიშნეთ, სუპერპოზიციის პრინციპს აპლიკაციების საკმაოდ ფართო სპექტრი აქვს. მისი ეფექტი ყველაზე ნათლად ჩანს ელექტროდინამიკაში. ამასთან, მნიშვნელოვანია გვახსოვდეს, რომ სუპერპოზიციის პრინციპის განხილვისას, ფიზიკა მას არ განიხილავს კონკრეტულ პოსტულატად, არამედ ელექტროდინამიკის თეორიის შედეგს.
მაგალითად, ელექტროსტატიკაში, ეს პრინციპი მოქმედებს, როდესაც მუხტების სისტემის შესწავლა კონკრეტულ წერტილში ქმნის დაძაბულობას, რომელიც იქნება თითოეული მუხტის ველის სიძლიერის ჯამი. ეს დასკვნა გამოიყენება პრაქტიკაში, რადგან მისი გამოყენება შესაძლებელია ელექტროსტატიკური ურთიერთქმედების პოტენციური ენერგიის გამოსათვლელად. ამ შემთხვევაში, საჭირო იქნება თითოეული ინდივიდუალური მუხტის პოტენციური ენერგიის გამოთვლა.
ამას ადასტურებს მაქსველის განტოლება, რომელიც წრფივია ვაკუუმში. ეს ასევე გულისხმობს იმ ფაქტს, რომ სინათლე არ იფანტება, არამედ ვრცელდება წრფივად, ამიტომ ცალკეული სხივები არ ურთიერთქმედებენ ერთმანეთთან. ფიზიკაში ამ ფენომენს ხშირად უწოდებენ სუპერპოზიციის პრინციპს ოპტიკაში.
აღსანიშნავია ისიც, რომ კლასიკურ ფიზიკაში სუპერპოზიციის პრინციპი გამომდინარეობს ცალკეული მოძრავი წრფივი სისტემების განტოლებების წრფივიდან და, შესაბამისად, არის მიახლოებითი. იგი ეფუძნება ღრმა დინამიურ პრინციპებს, მაგრამ მისი სიახლოვე არ ხდის მას არც უნივერსალურ და არც ფუნდამენტურს.
კერძოდ, ძლიერი აღწერილია სხვა განტოლებებით, არაწრფივი და, შესაბამისად, პრინციპი არ შეიძლება გამოყენებულ იქნას ამ სიტუაციებში. მაკროსკოპული ასევე არ ემორჩილება ამ პრინციპს, რადგან ეს დამოკიდებულია გარე ველების გავლენას.
თუმცა ძალების სუპერპოზიციის პრინციპი ფუნდამენტურია კვანტურ ფიზიკაში. თუ სხვა განყოფილებებში ის გამოიყენება გარკვეული შეცდომით, მაშინ კვანტურ დონეზე ის საკმაოდ ზუსტად მუშაობს. ნებისმიერი კვანტური მექანიკური სისტემა გამოსახულია წრფივი სივრცის ვექტორებიდან და თუ ის ემორჩილება წრფივ ფუნქციებს, მაშინ მისი მდგომარეობა განისაზღვრება სუპერპოზიციის პრინციპით, ე.ი. შედგება თითოეული მდგომარეობისა და ტალღური ფუნქციის სუპერპოზიციისგან.
განაცხადის შეზღუდვები საკმაოდ პირობითია. კლასიკური ელექტროდინამიკის განტოლებები წრფივია, მაგრამ ეს არ არის ფუნდამენტური წესი. ფიზიკის ფუნდამენტური თეორიები ეფუძნება არაწრფივ განტოლებებს. ეს ნიშნავს, რომ მათში სუპერპოზიციის პრინციპი არ შესრულდება; ეს მოიცავს ფარდობითობის ზოგად თეორიას, კვანტურ ქრომოდინამიკას და იანგ-მილსის თეორიას.
ზოგიერთ სისტემაში, სადაც წრფივობის პრინციპები მხოლოდ ნაწილობრივ გამოიყენება, სუპერპოზიციის პრინციპი ასევე შეიძლება პირობითად იქნას გამოყენებული, მაგალითად, სუსტი გრავიტაციული ურთიერთქმედებები. გარდა ამისა, ატომებისა და მოლეკულების ურთიერთქმედების განხილვისას, სუპერპოზიციის პრინციპი ასევე არ არის დაცული, ეს ხსნის მასალების ფიზიკური და ქიმიური თვისებების მრავალფეროვნებას.
სხეულები, რომლებსაც აქვთ გარკვეული მოცულობა და ხაზოვანი ზომები, ყოველთვის იკავებენ სივრცის ნაწილს, რომელშიც სხვა სხეულები არ შეიძლება განთავსდეს გარკვეული მახასიათებლების შეცვლის გარეშე. სადაც ქვა მდებარეობს, იქ არ შეიძლება იყოს სხვა ქვა, არც ლითონის ბურთი და არც რაიმე სხვა მატერიალური ობიექტი.
ელექტრული ველის დამახასიათებელი მახასიათებელია ის, რომ მატერიისგან განსხვავებით, სხვადასხვა წყაროდან და სხვადასხვა წარმოშობის ველები შეიძლება ერთდროულად იმყოფებოდეს სივრცის ერთ წერტილში. ამავდროულად, თითოეული სფერო ინარჩუნებს თავის ინდივიდუალობას და არც ერთი მახასიათებელი არ იცვლება სხვა სფეროს გავლენით. ამის ერთ-ერთი დადასტურებაა რადიოტალღების გავრცელების ცნობილი მაგალითი, რომლებიც წარმოადგენენ ალტერნატიულ ელექტრომაგნიტურ ველს. ჩრდილოეთიდან სამხრეთისკენ მიმავალი რადიოტალღა საერთოდ არ მოქმედებს დასავლეთიდან აღმოსავლეთისკენ მიმავალ ტალღაზე. და მსმენელი, რომელიც იღებს პირველ ტალღას მოტანილ ინფორმაციას, ვერც კი აცნობიერებს, რომ ეს ტალღა სხვას „შეხვედრია“.
მსგავსი რამ შეინიშნება იმ შემთხვევაში, როდესაც არსებობს დამუხტული სხეულების გარკვეული სისტემა და მათ შესაბამისი ველები.
დაე, იყოს დადებითი მუხტის მქონე სხეული A სივრცეში რაღაც წერტილში Q 1(სურ. 4.33). თუ დადებით მუხტის მქონე წერტილოვან სხეულს B თვითნებურ წერტილში შევიყვანთ q 0,მაშინ მასზე ძალა იმოქმედებს F̅ 1 B სხეულის A სხეულის ველთან ურთიერთქმედების შედეგად.
მუხტის მქონე სხეულს შევიყვანთ თვითნებურ C წერტილში Q 2(სურ. 4.34). მისი ველი იმოქმედებს B სხეულზე ძალით F 2.სიძლიერის მნიშვნელობაში ცვლილება არ არის F̅ 1 არ მოხდება. მაგრამ მექანიკიდან ცნობილია, რომ თუ სხეულზე მოქმედებს რამდენიმე ძალა, მაშინ ისინი შეიძლება შეიცვალოს შედეგიანით (სურ. 4.35).
რამდენიმე ელექტრული ველის წყაროს შემთხვევაში
F =F̅ 1 +ფ 2 + … + ფნ.
თუ განტოლების მარცხენა და მარჯვენა მხარეები იყოფა q 0,შემდეგ მივიღებთ
F̅ /q 0 =ფ 1 / q 0 + ფ 2 / q 0 + … + ფn/q 0,
ე = ე 1 + ე 2 + … + ენ.
შესაბამისად, დამუხტული სხეულის ურთიერთქმედების გაანგარიშებისას ელექტრულ ველებთან სხვადასხვა წყაროდან, შეიძლება გამოვიყენოთ „მთლიანი“ ელექტრული ველის ინტენსივობის კონცეფცია. ეს დასკვნა ჩამოყალიბებულია როგორც ველების სუპერპოზიციის პრინციპი.მასალა საიტიდან
ველების სუპერპოზიციის პრინციპი. დამუხტული სხეულების სისტემის ელექტრული ველის სიძლიერე ნებისმიერ წერტილში უდრის ამ წერტილში ცალკეული სხეულების ველის სიძლიერის ვექტორულ ჯამს.
მათემატიკური ფორმით, ეს პრინციპი იწერება შემდეგნაირად:
ე = ე 1 + ე 2 + … + ეn,
სად ე -დამუხტული სხეულების სისტემის ველის სიძლიერე; E̅ 1,2…- თითოეული სხეულის დაძაბულობა, რომელიც არის სისტემის ნაწილი.
სხეულის ელექტრული ველის სიძლიერე, რომელსაც აქვს დადებითად და უარყოფითად დამუხტული ნაწილაკების ერთნაირი რაოდენობა, ნულის ტოლია.
ველების სუპერპოზიციის პრინციპიარ შემოიფარგლება სისტემაში არსებული ორგანოების რაოდენობით. სწორედ ამიტომ, დაუმუხტველი სხეულის ელექტრული ველის სიძლიერე, რომელიც მოიცავს უზარმაზარ რაოდენობას დადებითი და უარყოფითი მუხტის მქონე ნაწილაკებს, პრაქტიკულად ნულის ტოლია.
ამ გვერდზე არის მასალა შემდეგ თემებზე:
როგორ არის ჩამოყალიბებული ველის სუპერპოზიციის პრინციპი?
ძალების სუპერპოზიციის პრინციპი ფორმულა
მოკლედ ელექტრული ველების სუპერპოზიციის პრინციპი
სუპერპოზიციის პრინციპის ფორმულა
რომელი გამონათქვამია ველის სუპერპოზიციის პრინციპის მათემატიკური გამოსახულება?
კითხვები ამ მასალის შესახებ:
ელექტროსტატიკის ერთ-ერთი მთავარი პრობლემაა ველის პარამეტრების შეფასება მოცემული, სტაციონარული, სივრცეში მუხტების განაწილებისთვის. ასეთი პრობლემების გადაჭრის ერთ-ერთი გზა ეფუძნება სუპერპოზიციის პრინციპი . მისი არსი შემდეგია.
თუ ველი იქმნება რამდენიმე წერტილის მუხტით, მაშინ საცდელ მუხტზე q მოქმედებს მუხტი qk ისეთივე ძალით, თითქოს სხვა მუხტები არ არსებობდეს. შედეგად მიღებული ძალა განისაზღვრება გამონათქვამით:
იმიტომ რომ , მაშინ არის მიღებული ველის სიძლიერე იმ წერტილში, სადაც სატესტო მუხტი მდებარეობს, ასევე ემორჩილება სუპერპოზიციის პრინციპს :
 |
(1.4.1) |
ეს ურთიერთობა გამოხატავს სუპერპოზიციის პრინციპს ან ელექტრული ველების სუპერპოზიცია და წარმოადგენს ელექტრული ველის მნიშვნელოვან თვისებას. შედეგად მიღებული ველის სიძლიერე, წერტილოვანი მუხტების სისტემა, უდრის თითოეულ მათგანს ცალ-ცალკე მოცემულ წერტილში შექმნილი ველის სიძლიერის ვექტორულ ჯამს.
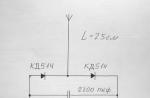
განვიხილოთ სუპერპოზიციის პრინციპის გამოყენება ორი მუხტის ელექტრული სისტემის მიერ შექმნილი ველის შემთხვევაში, მუხტებს შორის მანძილით ტოლი ლ(ნახ. 1.2).
ბრინჯი. 1.2
სხვადასხვა მუხტის მიერ შექმნილი ველები არ ახდენენ გავლენას ერთმანეთზე, ამიტომ რამდენიმე მუხტის შედეგად მიღებული ველის ვექტორი შეიძლება ვიპოვოთ ვექტორის დამატების წესის გამოყენებით (პარალელოგრამის წესი)
 .
|
Ამ შემთხვევაში
და 
აქედან გამომდინარე,
 |
(1.4.2) |
მოდით შევხედოთ სხვა მაგალითს. მოდი ვიპოვოთ ელექტროსტატიკური ველის სიძლიერე ეშექმნილი ორი დადებითი მუხტით q 1და q 2წერტილში ა, მდებარეობს მანძილზე r 1პირველიდან და r 2მეორე მუხტიდან (სურ. 1.3).
ბრინჯი. 1.3
გამოვიყენოთ კოსინუსების თეორემა:
| (1.4.3) |
სად 
.
თუ ველი შეიქმნა არა წერტილის გადასახადი, შემდეგ გამოიყენეთ ჩვეულებრივი ტექნიკა ასეთ შემთხვევებში. სხეული იყოფა უსასრულოდ მცირე ელემენტებად და განისაზღვრება თითოეული ელემენტის მიერ შექმნილი ველის სიძლიერე, შემდეგ ინტეგრირებული მთელ სხეულზე:
| (1.4.4) |
სად არის ველის სიძლიერე დამუხტული ელემენტის გამო. ინტეგრალი შეიძლება იყოს წრფივი, ფართობზე ან მოცულობაზე, სხეულის ფორმის მიხედვით. ასეთი პრობლემების გადასაჭრელად გამოიყენეთ მუხტის სიმკვრივის შესაბამისი მნიშვნელობები:
– წრფივი მუხტის სიმკვრივე, გაზომილი C/m-ში;
– ზედაპირული მუხტის სიმკვრივე, გაზომილი C/m2-ში;
– მოცულობითი მუხტის სიმკვრივე, გაზომილი C/m3-ში.
თუ ველი იქმნება რთული ფორმის დამუხტული სხეულებით და არათანაბრად დამუხტული, მაშინ სუპერპოზიციის პრინციპის გამოყენებით, ძნელია მიღებული ველის პოვნა.
ფორმულა (1.4.4) ჩვენ ვხედავთ, რომ არის ვექტორული რაოდენობა:
 |
(1.4.5) |
ასე რომ, ინტეგრაცია შეიძლება არ იყოს ადვილი. ამიტომ, გამოთვლებისთვის ხშირად გამოიყენება სხვა მეთოდები, რომლებსაც შემდეგ თემებში ვისაუბრებთ. თუმცა, ზოგიერთ შედარებით მარტივ შემთხვევაში, ეს ფორმულები შესაძლებელს ხდის ანალიზურ გამოთვლას.
მაგალითებად შეგვიძლია განვიხილოთ მუხტის წრფივი განაწილება ან წრიული მუხტის განაწილება.
მოდით განვსაზღვროთ ელექტრული ველის სიძლიერე ერთ წერტილში ა(ნახ. 1.4) x მანძილზე უსასრულოდ გრძელი, წრფივი, თანაბრად განაწილებული მუხტიდან. მოდით λ იყოს მუხტი სიგრძის ერთეულზე.
ბრინჯი. 1.4
ჩვენ ვვარაუდობთ, რომ x მცირეა გამტარის სიგრძესთან შედარებით. ავირჩიოთ კოორდინატთა სისტემა ისე, რომ y ღერძი ემთხვევა გამტარს. სიგრძის ელემენტი დი, ატარებს მუხტს ამ ელემენტის მიერ შექმნილ ელექტრული ველის სიძლიერე წერტილში ა.
| , |
სადაც = არის ვექტორი, რომელიც მიმართულებით ემთხვევა ზედაპირის ნორმალურს (ზედაპირის ნორმალურის ერთეული ვექტორი) და სიდიდით უდრის ფართობს. ვინაიდან ინტეგრალი არის ვექტორების სკალარული პროდუქტი, ნაკადი შეიძლება იყოს დადებითი ან უარყოფითი, ვექტორის მიმართულების არჩევის მიხედვით. გეომეტრიულად, დინება პროპორციულია მოცემულ ტერიტორიაზე შეღწევადი ელექტროგადამცემი ხაზების რაოდენობისა (იხ. ნახ. 2.3.1).
გაუსის თეორემა.
ელექტრული ველის სიძლიერის ვექტორის ნაკადი თვითნებური გზით
დახურული ზედაპირი უდრის თანდართული მუხტების ალგებრულ ჯამს
ამ ზედაპირის შიგნით იყოფა(SI სისტემაში)
| . (2.3.1) |
დახურული ზედაპირის შემთხვევაში ვექტორი არჩეულია ზედაპირიდან გარედან.
ამრიგად, თუ ძალის ხაზები ტოვებენ ზედაპირს, ნაკადი დადებითი იქნება, ხოლო თუ ისინი შედიან, მაშინ უარყოფითი.
ელექტრული ველების გამოთვლა გაუსის თეორემის გამოყენებით.
რიგ შემთხვევებში, ელექტრული ველის სიძლიერე გამოითვლება გაუსის თეორემის გამოყენებით
ეს საკმაოდ მარტივია. თუმცა, ის ემყარება სუპერპოზიციის პრინციპს.
ვინაიდან წერტილის მუხტის ველი ცენტრალურად სიმეტრიულია, მაშინ ველი
მუხტების ცენტრალური სიმეტრიული სისტემა ასევე იქნება ცენტრალიზებული სიმეტრიული. უმარტივესი მაგალითია ერთნაირად დამუხტული ბურთის ველი. თუ მუხტის განაწილებას აქვს ღერძული სიმეტრია, მაშინ ველის სტრუქტურა ასევე განსხვავდება ღერძულ სიმეტრიაში. მაგალითი იქნება უსასრულო ერთნაირად დამუხტული ძაფი ან ცილინდრი. თუ მუხტი თანაბრად ნაწილდება უსასრულო სიბრტყეზე, მაშინ ველის ხაზები განლაგდება სიმეტრიულად მუხტის სიმეტრიის მიმართ. ამრიგად, გამოთვლის ეს მეთოდი გამოიყენება მუხტის განაწილების მაღალი ხარისხის სიმეტრიის შემთხვევაში, რომელიც ქმნის ველებს. ქვემოთ მოცემულია ასეთი ველების გამოთვლის მაგალითები.
ერთნაირად დამუხტული ბურთის ელექტრული ველი.
რადიუსის ბურთი თანაბრად არის დამუხტული მოცულობის სიმკვრივით. მოდით გამოვთვალოთ ველი ბურთის შიგნით.
დამუხტვის სისტემა ცენტრალურად სიმეტრიულია. IN
როგორც ინტეგრაციის ზედაპირი, რომელსაც ჩვენ ვირჩევთ
რადიუსის სფერო რ(რ<რ), რომლის ცენტრი ემთხვევა
მუხტის სიმეტრიის ცენტრთან (იხ. ნახ. 2.3.2). მოდით გამოვთვალოთ ვექტორული ნაკადი ამ ზედაპირზე.
ვექტორი მიმართულია რადიუსის გასწვრივ. მინდორიდან მოყოლებული
აქვს ცენტრალური სიმეტრია, მაშინ
მნიშვნელობა ეყველა პუნქტში იგივე იქნება
შერჩეული ზედაპირი. მერე
ახლა ვიპოვოთ მუხტი შერჩეული ზედაპირის შიგნით
გაითვალისწინეთ, რომ თუ მუხტი ნაწილდება არა ბურთის მთელ მოცულობაზე, არამედ მხოლოდ მის ზედაპირზე (მოცემულია დამუხტული მუხტი სფერო), მაშინ ველის სიძლიერე შიგნით იქნება ნულის ტოლი.
მოდით გამოვთვალოთ ველი ბურთის გარეთიხილეთ ნახ. 2.3.3.
ახლა ინტეგრაციის ზედაპირი მთლიანად ფარავს ბურთის მთელ მუხტს. გაუსის თეორემა დაიწერება ფორმით
გავითვალისწინოთ, რომ ველი ცენტრალურად სიმეტრიულია
და ბოლოს, დატვირთული ბურთის გარეთ ველის სიძლიერისთვის ვიღებთ
ამრიგად, ერთნაირად დამუხტული ბურთის გარეთ მინდორს ექნება იგივე ფორმა, რაც ბურთის ცენტრში მოთავსებულ წერტილოვან მუხტს. იგივე შედეგს ვიღებთ ერთნაირად დამუხტული სფეროსთვის.
მიღებული შედეგის (2.3.2) და (2.3.3) ანალიზი შეგიძლიათ ნახ. 2.3.4 გრაფიკის გამოყენებით.
უსასრულო თანაბრად დამუხტული ცილინდრის ელექტრული ველი.
მოდით, უსასრულოდ გრძელი ცილინდრი თანაბრად იყოს დამუხტული მოცულობითი სიმკვრივით.
ცილინდრის რადიუსი არის. მოდი ვიპოვოთ ველი ცილინდრის შიგნით, როგორც ფუნქცია
მანძილი ღერძიდან. ვინაიდან მუხტების სისტემას აქვს ღერძული სიმეტრია,
მოდით ასევე გონებრივად ავირჩიოთ უფრო პატარა ცილინდრი, როგორც ინტეგრაციის ზედაპირი
რადიუსი და თვითნებური სიმაღლე, რომლის ღერძი ემთხვევა ამოცანის სიმეტრიის ღერძს (სურ. 2.3.5). მოდით გამოვთვალოთ დინება ამ ცილინდრის ზედაპირზე, გავყოთ იგი ინტეგრად გვერდითი ზედაპირზე.
და საფუძველი
სიმეტრიის მიზეზების გამო
აქედან გამომდინარეობს, რომ იგი მიმართულია რადიალურად. შემდეგ, ვინაიდან ველის ხაზები არ შეაღწევს არჩეული ცილინდრის არცერთ ფუძეს, ამ ზედაპირებზე ნაკადი ნულის ტოლია. ვექტორული ნაკადი ცილინდრის გვერდითი ზედაპირის გავლით დაიწერება:
მოდით ჩავანაცვლოთ ორივე გამონათქვამი გაუსის თეორემის თავდაპირველ ფორმულაში (2.3.1)
მარტივი გარდაქმნების შემდეგ ვიღებთ გამონათქვამს ცილინდრის შიგნით ელექტრული ველის სიძლიერისთვის
ამ შემთხვევაშიც, თუ მუხტი ნაწილდება მხოლოდ ცილინდრის ზედაპირზე, მაშინ შიგნით ველის სიძლიერე ნულის ტოლია.
ახლა მოდი ვიპოვოთ ველი გარეთდამუხტული ცილინდრი
გონებრივად ავირჩევთ ზედაპირად, რომლის მეშვეობითაც გამოვთვლით ვექტორის ნაკადს, რადიუსის და თვითნებური სიმაღლის ცილინდრის (იხ. სურ. 2.3.6).
ნაკადი ჩაიწერება ისევე, როგორც შიდა ზონისთვის. და გონებრივი ცილინდრის შიგნით არსებული მუხტი ტოლი იქნება:
მარტივი გარდაქმნების შემდეგ ვიღებთ გამონათქვამს ელექტრული ძაბვისთვის
ველები დამუხტული ცილინდრის გარეთ:
თუ ამ პრობლემაში შემოვიყვანთ მუხტის წრფივ სიმკვრივეს, ე.ი. დამუხტვა ცილინდრის სიგრძის ერთეულზე, შემდეგ გამოხატულება (2.3.5) გარდაიქმნება ფორმაში
რომელიც შეესაბამება სუპერპოზიციის პრინციპით მიღებულ შედეგს (2.2.14).
როგორც ვხედავთ, გამონათქვამებში (2.3.4) და (2.3.5) დამოკიდებულებები განსხვავებულია. მოდით ავაშენოთ გრაფიკი.
უსასრულო ერთნაირად დამუხტული სიბრტყის ველი .
უსასრულო სიბრტყე ერთნაირად დატვირთულია ზედაპირის სიმკვრივით. ელექტრული ველის ხაზები სიმეტრიულია ამ სიბრტყის მიმართ და, შესაბამისად, ვექტორი დამუხტული სიბრტყის პერპენდიკულარულია. გონებრივად შევარჩიოთ თვითნებური განზომილების ცილინდრი ინტეგრაციისთვის და მოვაწყოთ ისე, როგორც ნაჩვენებია ნახ. 2.3.8. ჩამოვწეროთ გაუსის თეორემა:) მისი შემოღება შეიძლება მოსახერხებელი იყოს სკალარულიმახასიათებლები ცვლილებები სფეროში, რომელსაც ეწოდება დივერგენცია.ამ მახასიათებლის დასადგენად, ჩვენ ვირჩევთ მცირე მოცულობას ველში გარკვეულ წერტილთან ახლოს რდა იპოვნეთ ვექტორული ნაკადი ამ მოცულობის შემოსაზღვრულ ზედაპირზე. შემდეგ ჩვენ ვყოფთ მიღებულ მნიშვნელობას მოცულობაზე და ვიღებთ შედეგად მიღებული თანაფარდობის ზღვარს, როდესაც მოცულობა იკუმშება მოცემულ წერტილში. რ. შედეგად მიღებული მნიშვნელობა ეწოდება ვექტორული განსხვავება
. (2.3.7)
ნათქვამიდან გამომდინარეობს. (2.3.8)
ეს თანაფარდობა ე.წ გაუს-ოსტროგრადსკის თეორემა, ის მოქმედებს ნებისმიერ ვექტორულ ველზე.
შემდეგ (2.3.1) და (2.3.8)-დან, იმის გათვალისწინებით, რომ მოცულობა შეიცავს V,შეგვიძლია დავწეროთ მივიღებთ
ან, რადგან განტოლების ორივე მხარეს ინტეგრალი აღებულია იმავე მოცულობაზე,
ეს განტოლება გამოხატავს მათემატიკურად გაუსის თეორემა ელექტრული ველის დიფერენციალური ფორმით.
დივერგენციის ოპერაციის მნიშვნელობა არის ის, რომ იგი ადგენს საველე წყაროების არსებობას (ველის ხაზების წყაროები). წერტილები, რომლებშიც განსხვავება არ არის ნულოვანი, არის ველის ხაზების წყარო. ამრიგად, ელექტროსტატიკური ველის ხაზები იწყება და მთავრდება მუხტებზე.
