ЛЕКЦИЯ 6-7. Элементы аналитической геометрии.

Поверхности и их уравнения.

Пример 1.

Сфера .

Пример 2.

F(x,y,z)=0 (*),

Это - уравнение поверхности

Примеры :

x 2 + y 2 – z 2 = 0 (конус)

Плоскость.

Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

Рассмотрим плоскость в пространстве. Пусть М 0 (x 0 , y 0 , z 0) – данная точка плоскости Р, а - вектор, перпендикулярный плоскости (нормальный вектор плоскости).

(1) – векторное уравнение плоскости.

В координатной форме:

A(x - x 0) + B(y - y 0) + C(z - z 0) = 0 (2)

Получили уравнение плоскости, проходящей через заданную точку .

Общее уравнение плоскости.

Раскроем скобки в (2): Ax + By + Cz + (-Ax 0 – By 0 – Cz 0) = 0 или

Ax + By + Cz + D = 0 (3)

Полученное уравнение плоскости линейно , т.е. уравнение 1 степени относительно координат x, y, z. Поэтому плоскость – поверхность первого порядка .

Утверждение : Всякое уравнение, линейное относительно x, y, z задает плоскость.

Любая плоскость м.б. задана уравнением (3), которое называется общим уравнением плоскости.

Частные случаи общего уравнения.

а) D=0: Ax + By + Cz = 0. Т.к. координаты точки О(0, 0, 0) удовлетворяют этому уравнению, то заданная им плоскость проходит через начало координат.

б) С=0: Ax + By + D = 0. В этом случае нормальный вектор плоскости , поэтому плоскость, заданная уравнением параллельна оси OZ.

в) С=D=0: Ax + By = 0. Плоскость параллельна оси OZ (т.к. С=0) и проходит через начало координат (т.к. D=0). Значит, она проходит через ось OZ.

г) В=С=0: Ax + D = 0 или . Вектор , т.е. и . Следовательно, плоскость параллельна осям OY и OZ, т.е. параллельна плоскости YOZ и проходит через точку .

Самостоятельно рассмотреть случаи: B=0, B=D=0, A=0, A=D=0, A=C=0, A=B=0/

Уравнение плоскости, проходящей через три заданные точки.

Т.к. все четыре точки принадлежат плоскости, то данные векторы компланарны, т.е. их смешанное произведение равно нулю:

Получили уравнение плоскости, проходящей через три точки в векторной форме.

В координатной форме:

(7)

Если раскрыть определитель, то получим уравнение плоскости в виде:

Ax + By + Cz + D = 0.

Пример . Написать уравнение плоскости, проходящей через точки М 1 (1,-1,0);

М 2 (-2,3,1) и М 3 (0,0,1).

, (x - 1)·3 - (y + 1)(-2) + z·1 = 0;

3x + 2y + z – 1 = 0.

Уравнение плоскости в отрезках

Пусть дано общее уравнение плоскости Ax + By + Cz + D = 0 и D ≠ 0, т.е. плоскость не проходит через начало координат. Разделим обе части на –D: и обозначим: ; ; . Тогда

получили уравнение плоскости в отрезках .

где a, b, c – величины отрезков, отсекаемых плоскостью на осях координат.

Пример 1. Написать уравнение плоскости, проходящей через точки А(3, 0, 0);

B(0, 2, 0) и С(0, 0, -3).

a=3; b=2; c=-3 , или 2x + 3y - 2z – 6 = 0.

Пример 2. Найти величины отрезков, которые отсекает плоскость

4x – y – 3z – 12 = 0 на осях координат.

4x – y – 3z = 12 a=3, b=-12, c=-4.

Нормальное уравнение плоскости.

Пусть дана некоторая плоскость Q. Из начала координат проведем перпендикуляр ОР к плоскости. Пусть заданы |ОР|=р и вектор : . Возьмем текущую точку M(x, y, z) плоскости и вычислим скалярное произведение векторов и : .

Если спроектировать точку М на направление , то попадем в точку Р. Т.о., получим уравнение

(9).

Задание линии в пространстве.

Линию L в пространстве можно задать как пересечение двух поверхностей. Пусть точка M(x, y, z), лежащая на линии L, принадлежит как поверхности Р1, так и поверхности Р2. Тогда координаты этой точки должны удовлетворять уравнениям обеих поверхностей. Поэтому под уравнением линии L в пространстве понимают совокупность двух уравнений, каждое из которых является уравнением соответствующей поверхности:

Линии L принадлежат те и только те точки, координаты которых удовлетворяют обоим уравнениям в (*). Позже мы рассмотрим и другие способы задания линий в пространстве.

Пучок плоскостей.

Пучок плоскостей – множество всех плоскостей, проходящих через заданную прямую – ось пучка.

Чтобы задать пучок плоскостей, достаточно задать его ось. Пусть уравнение этой прямой задано в общем виде:

.

Составить уравнение пучка – значит составить уравнение, из которого можно получить при дополнительном условии уравнение любой плоскости пучка, кроме, б.м. одной. Умножим II уравнение на л и сложим с I уравнением:

A 1 x + B 1 y + C 1 z + D 1 + л(A 2 x + B 2 y + C 2 z + D 2) = 0 (1) или

(A 1 + лA 2)x + (B 1 + лB 2)y + (C 1 + лC 2)z + (D 1 + лD 2) = 0 (2).

л – параметр – число, которое может принимать действительные значения. При любом выбранном значении л уравнения (1) и (2) линейные, т.е. это – уравнения некоторой плоскости.

1. Покажем , что эта плоскость проходит через ось пучка L. Возьмем произвольную точку M 0 (x 0 , y 0 , z 0) L. Следовательно, М 0 Р 1 и М 0 Р 2 . Значит:

Следовательно, плоскость, описываемая уравнением (1) или (2) принадлежит пучку.

2. Можно доказать и обратное : всякая плоскость, проходящая через прямую L, описывается уравнением (1) при соответствующем выборе параметра л.

Пример 1 . Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + y + 5z – 1 = 0 и 2x + 3y – z + 2 = 0 и через точку М(3, 2, 1).

Записываем уравнение пучка: x + y + 5z – 1 + л(2x + 3y – z + 2) = 0. Для нахождения л учтем, что М Р:

Всякую поверхность в пространстве можно рассматривать как геометрическое место точек, обладающим некоторым свойством, общим для всех точек.

Пример 1.

Сфера – множество точек, равноудаленных от данной точки С (центра). С(x 0 ,y 0 ,z 0). По определению |СМ|=R или или . Данное уравнение выполняется для всех точек сферы и только для них. Если x 0 =0, y 0 =0, z 0 =0, то .

Аналогичным образом можно составить уравнение любой поверхности, если выбрана система координат.

Пример 2. x=0 – уравнение плоскости YOZ.

Выразив геометрическое определение поверхности через координаты ее текущей точки и собрав все слагаемые в одной части, получим равенство вида

F(x,y,z)=0 (*),

Это - уравнение поверхности , если координаты всех точек поверхности удовлетворяют данному равенству, а координаты точек, не лежащих на поверхности, не удовлетворяют.

Т.о., каждой поверхности в выбранной системе координат соответствует свое уравнение. Однако, не каждому уравнению вида (*) соответствует поверхность в смысле определения.

Примеры :

2x – y + z – 3 = 0 (плоскость)

x 2 + y 2 – z 2 = 0 (конус)

x 2 + y 2 +3 = 0 – координаты ни одной точки не удовлетворяют.

x 2 + y 2 + z 2 =0 – единственная точка (0,0,0).

x 2 = 3y 2 = 0 – прямая (ось OZ).

Уравнение
поверхности
F(x,y,z)=0
.

Плоскость. Уравнение плоскости по точке и нормальному вектору

Положение плоскости в пространстве
можно определить, задав какую-либо
точку М0 на плоскости и какой-либо
нормальный вектор. Нормальным
вектором плоскости называется любой
вектор, перпендикулярный к этой
плоскости.

Пусть точка М0(х0,у0,z0) лежит в плоскости.
Введем в рассмотрение произвольную точку
плоскости М(х,у,z).
z
n (A,B,C)
M
y
M0
x

Векторы n(A, B, C) и M 0 M (x x0 , y y0 , z z0)
ортогональны.
A(x-x0)+B(y-y0)+C(z-z0)=0
Уравнение плоскости по точке и
нормальному вектору.

Пример 1:

проходящей через точку М(2,3,-1)
перпендикулярно вектору n(1,2, 3)
Решение:
По формуле: 1(х-2)+2(у-3)-3(z+1)=0
или х+2у-3z-11=0

Пример 2:
Написать уравнение плоскости,
проходящей через точку М(1,0,0)
перпендикулярно вектору n(2,0,1) .
Решение:
Получаем: 2(х-1)+0(у-0)+1(z-0)=0
или 2х+z-2=0.

Общее уравнение плоскости

A(x-x0)+B(y-y0)+C(z-z0)=0, раскроем в нем
скобки и обозначим –Aх0-Ву0-Сz0=D.
Приведем уравнение рассматриваемой
плоскости к виду:
Ax+By+Cz+D=0 - общее уравнение плоскости.
Коэффициенты А,В,С являются
координатами нормального вектора
плоскости.

Частные случаи общего уравнения плоскости

1. Пусть А=0, В,С,D≠0. Тогда: By+Cz+D=0.
Нормальный вектор плоскости n(0, B, C)
перпендикулярен оси ОХ и, следовательно,
плоскость параллельна оси ОХ.
z
y
x

Уравнения Ax+Cz+D=0 и Ax+By+D=0
выражают плоскости, параллельные осям ОУ
и OZ.
2. D=0, А,В,С≠0. Уравнение плоскости:
Ax+By+Cz=0. Точка О(0,0,0) удовлетворяет
уравнению плоскости. Уравнение задает
плоскость, проходящую через начало
координат.
3. А=0, D=0, В,С≠0. Уравнение плоскости:
By+Cz=0. Плоскость одновременно
параллельна оси ОХ и проходит через начало
координат, т.е. проходит через ось ОХ.

Аналогично уравнения Ax+Cz=0 и Ax+By=0
выражают плоскости, проходящие через оси
OY и OZ.
4. А=0, В=0, С,D≠0. Уравнение плоскости:
Cz+D=0. Плоскость одновременно
параллельна осям ОХ и ОУ, т.е. координатной
плоскости ОХУ. Аналогично уравнения
By+D=0, и Ax+D=0 выражают плоскости,
параллельные координатным плоскостям OXZ
и OYZ.

Пример:
Z=3
z
3
y
x

А=0, В=0, D=0, С≠0.
Уравнение плоскости: Cz=0 или z=0. Это
плоскость одновременно параллельная
координатной плоскости ОХУ, т.е. сама
координатная плоскость ОХУ. Аналогично:
у=0 и х=0 – уравнения координатных
плоскостей OXZ и OYZ.

Уравнение плоскости, проходящей через три заданные точки

Три точки, не лежащие на одной прямойM1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3).
M(x,y,z) – произвольная точка плоскости.
z
M2
М1
М3
М

Векторы M1M , M 1M 2 , M 1 M 3 ,
компланарны. Их смешанное
произведение равно нулю.
x x1
x2 x1
y y1
y2 y1
z z1
z 2 z1 0
x3 x1
y3 y1
z3 z1
Это искомое уравнение плоскости,
проходящей через три заданные точки.

Пример. Написать уравнение плоскости,
проходящей через точки M1(1,2,1),
M2(0,1,4), M3(-3,3,2).
Решение: Используя полученное
уравнение, имеем:
x 1 y 2 z 1
1
4
2
1
3 0
1
Или 4х+11у+5z-31=0

Угол между плоскостями, условие параллельности и перпендикулярности двух плоскостей

Две плоскости: A1x+B1y+C1z+D1=0 и
A2x+B2y+C2z+D2=0. Их нормальные
векторы n1 (A1 , B1 , C1) , n2 (A2 , B2 , C2)
Углом между двумя плоскостями
называется угол между их нормальными
векторами
n1 n2
Cosω=
n1 n2
A1 A2 B1 B2 C1C2
A12 B12 C12 A22 B22 C22

Если плоскости перпендикулярны, то их
нормальные векторы тоже
перпендикулярны, и поэтому их
скалярное произведение равно нулю:
А1·А2+В1·В2+С1·С2=0.
Если плоскости параллельны, то
параллельны их нормальные векторы, а
значит, выполняются соотношения:
A1 B1 C1
A2 B2 C2

Пример: Написать уравнение плоскости,
проходящей через точку M(0,1,4)
параллельно плоскости 2х-4у-z+1=0.
Решение: Вектор нормали данной
плоскости будет являться нормальным
вектором и для искомой плоскости.
Используем уравнение плоскости по точке
и нормальному вектору:
2(х-0)-4(у-1)-(z-4)=0 или 2х-4у-z+8=0.

.Расстояние от точки до плоскости

найти расстояние от точки М(х0,у0,z0) до
плоскости: Ax+By+Cz+D=0. Опустим из точки
М перпендикуляр МК на плоскость (d).
z
M
n
K
x
y

Пусть точка К имеет координаты х1,у1,z1
n KM n KM d n
Или n KM А(х0-х1)+В(у0-у1)+С(z0-z1)=
= Ax0+By0+Cz0-(Ax1+By1+Cz1).
Точка К лежит в плоскости, ее
координаты удовлетворяют уравнению
плоскости, то есть Ax1+By1+Cz1+D=0.

Учитывая это, получаем: n KM
Ax0+By0+Cz0+D-(Ax1+By1+Cz1+D)=
Ax0+By0+Cz0+D.
Тогда: Ax0+By0+Cz0+D= d n ;
d
Ax0 By 0 Cz0 D
A B C
2
2
2

Пример:
Найти расстояние от точки М (-1,2,3) до
плоскости 2х-6у-3z+2=0.
Решение:
Воспользуемся формулой и подставим в
уравнение плоскости координаты
заданной точки:
d
2 (1) (6) 2 3 (3) 2
2 2 (6) 2 32
21
=
=3
7

Общие уравнения прямой в пространстве

Прямая в пространстве рассматривается
как линия пересечения двух плоскостей.
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
Система задает прямую в том случае, если
плоскости не являются параллельными,
A1 B1 C1
A2 B2 C 2

Канонические уравнения прямой в пространстве

Положение прямой L в пространстве
однозначно определено, если известна
какая-нибудь точка М0(х0,у0,z0), лежащая на
прямой L, и задан направляющий вектор
S (m, n, p)
S
M
M0

М(х,у,z) – произвольная точка на этой
прямой. Тогда векторы
M 0 M =(х-х0, у-у0, z-z0) и S (m, n, p)
будут коллинеарны:
x x0 y y 0 z z 0
m
n
p
- канонические уравнения прямой в
пространстве или уравнения прямой по
точке и направляющему вектору.

Пример 1:

через точку М(1,2,3), параллельно прямой
x 1 y 7 z
2
5
3
Решение:
Так как прямые параллельны, то S (2,5,3)
является направляющим вектором и искомой
прямой. Следовательно:
x 1 y 2 z 3
2
5
3

Пример 2:
Написать уравнение прямой L, проходящей
через точку М(1,2,3), и имеющей
направляющий вектор S (2,0,5)
Решение:
Воспользуемся формулой:
x 1 z 3
и
2
5
у-2=0,
то есть 5х-2z+1=0 и у=2. Это означает, что
прямая лежит в плоскости у=2

Уравнения прямой в пространстве по двум точкам

Заданы две точки М1(х1,у1,z1) и М2(х2,у2,z2).
Написать уравнение прямой, проходящей
через две точки.
М1
М2

Прямая проходит через точку М1 и имеет в
качестве направляющего вектора M 1M 2
Уравнение имеет вид:
x x1
y y1
z z1
x2 x1 y 2 y1 z 2 z1
Пример: Написать уравнение прямой,
проходящей через точки М1(1,4,-3) и
М2(2,1,1).
Решение: Воспользуемся формулой
x 2 y 1 z 1
1
3
4

Параметрические уравнения прямой в пространстве

Рассмотрим канонические уравнения
прямой: x x0 y y0 z z 0
m
n
p
Введем параметр t:
x x0 y y 0 z z 0
t
m
n
p
-∞ < t <+∞.

Получим:
x x0
t
y m y
0
t
n
z z0 t
p
или
x x0 mt
y y0 nt
z z pt
0
параметрические уравнения прямой в
пространстве. В таком виде их часто
используют в механике и физике, параметр t,
обычно, время.

Приведение общих уравнений прямой в пространстве к каноническому виду

Заданы общие уравнения прямой в
пространстве
A1 x B1 y C1 z D1 0 (1)
A2 x B2 y C2 z D2 0
Привести их к каноническому виду
x x0 y y 0 z z 0
m
n
p

Для решения задачи нужно:
1. найти координаты (х0,у0,z0) какой-либо
точки, лежащей на прямой,
2. найти координаты (m,n,p) направляющего
вектора этой прямой.
Чтобы найти координаты точки М0 придадим
одной из координат произвольное численное
значение, например полагаем х=х0. Внеся его
в систему (1), получаем систему двух
уравнений с неизвестными у и z. Решаем ее.
В результате на прямой найдена точка
М0(х0,у0,z0).

В качестве направляющего вектора примем
вектор, который является результатом
векторного произведения нормальных
векторов двух плоскостей.
S (m, n, p) n1 n2
i
A1
j
B1
A2
B2
k
B1
C1
B2
C2
C1
C2
i
A1
C1
A2
C2
j
A1
B1
A2
B2
k

Получаем координаты направляющего
вектора:
A1 B1
A1 C1
B1 C1
p
n
m
A2 B2
A2 C2
B2 C2
Общие уравнения прямой, записанные в
каноническом виде:
x x0
y y0
z z0
B1 C1
C1 A1
A1 B1
B2
C2
C2
A2
A2
B2

Пример: Записать каноническое уравнение
прямой
x 2 y z 5 0
x y z 1 0
Решение: Положим z0=0. Тогда:
x 2 y 5
x y 1
Отсюда: : у0=-6, х0=7. Точка М0, лежащая на
прямой, имеет координаты: (7,-6,0).

Найдем направляющий вектор. Нормальные
векторы плоскостей имеют координаты
n1 (1,2, 1)
Тогда
n2 (1,1,1)
i j k
S n1 n2 1 2 1 3i 2 j k
1 1
1
Канонические уравнения прямой имеют вид:
x 7 y 6 z
3
2
1

Угол между двумя прямыми в пространстве, условие перпендикулярности и параллельности прямых

прямые L1 и L2 заданы в каноническом виде с
направляющими векторами
S 1 (m1 , n1 , p1) и S 2 (m2 , n2 , p2)
x x1 y y1 z z1
m1
n1
p1
x x2 y y 2 z z 2
m2
n2
p2

Углом между двумя прямыми называется угол
между их направляющими векторами.
S1 S 2
cos (L1 , L2) cos(S1 , S 2)
S1 S 2
cos(L1 , L2)
m1m2 n1n2 p1 p2
m12 n12 p12 m22 n22 p22

Прямые перпендикулярны, если
перпендикулярны их направляющие векторы:
То есть S1 S2 0 , или
m1m2+n1n2+p1p2=0.
Прямые параллельны, если параллельны их
направляющие векторы:
m1 n1
p1
m2 n 2 p 2

Пример: Найти угол между прямыми
x 2 y 7
z
1
3
2
и
x 10 y 3 z 5
4
1
2
Решение: Направляющие векторы прямых
имеют координаты: (1,3,-2) и (4,1,2).
Следовательно,
1 4 3 1 (2) 2
3
cos(L1 , L2)
1 9 4 16 1 4 7 16
3
(L1 , L2) arccos
7 16

Угол между прямой и плоскостью

Задана плоскость Р: Ах+Ву+Сz+D=0, и
прямая L:
x x0 y y 0 z z 0
m
n
p
n
S
ω
φ

Углом между прямой и плоскостью
называется угол φ между прямой и проекцией
ее на плоскость.
ω - угол между нормальным вектором
плоскости и направляющим вектором
прямой. ω=π/2-φ. Тогда sinφ=cos(π/2-φ)=
=cosω. Но cosω=cos (n, S)
Тогда
n S
sinφ= cos (n, S)
n S

sinφ =
Am Bn Cp
m 2 n 2 p 2 A2 B 2 C 2
Пример: Найти угол между прямой:
x 2 y 1 z
3
2
6
и плоскостью: 2х+у+2z-5=0.
Решение: Нормальный вектор плоскости
имеет координаты: (2,1,2), направляющий
вектор прямой имеет координаты: (3,2,-6).
sin
6 2 12
4
2
2
2
2
2
2
21
2 1 2 3 2 6

Условие перпендикулярности и параллельности прямой и плоскости.

x x0 y y 0 z z 0
m
n
p
P
Задана прямая L:
и плоскость Р: Ах+Ву+Сz+D=0.
Если прямая параллельна плоскости, то
направляющий вектор прямой
перпендикулярен нормальному вектору
плоскости.
S
n
L

Следовательно, их скалярное произведение
равно нулю: A·m+B·n+C·p=0.
Если прямая перпендикулярна плоскости, то
эти векторы параллельны.
S
n
Р
L
В этом случае:
A B C
m n p

Пример:
Написать уравнение прямой,
проходящей через точку М(1,2,-3),
перпендикулярно плоскости
4х+2у-z+5=0.
Решение:
Так как плоскость перпендикулярна
прямой, то нормальный вектор и
направляющий вектор параллельны:
x 1 y 2 z 3
4
2
1

Разберем типовую задачу.
Даны вершины пирамиды ABCD: А(1,0,0);
B(0,2,0); C(0,0,3), D(2,3,4). Найти:
1. Длину и уравнение ребра АВ,
2. Уравнение и площадь грани АВС,
3. Уравнение и длину высоты, опущенной
из вершины D на грань АВС,
4. Угол между ребром AD и гранью АВС,
5. Объем пирамиды.

Чертеж:
z
D
C
B
A
x
y

1. Введем в рассмотрение вектор AB . Его
координаты: (0-1;2-0;0-0), или (-1;2;0). Длина
ребра АВ равна модулю вектора.
АВ= 1 4 0 5
Уравнение прямой АВ (уравнение прямой по
двум точкам):
x 1 y
1 2
Или 2х+у-2=0

2. Уравнение грани АВС (уравнение
плоскости по трем точкам):
x 1 y z
1 2 0 0
1
0 3
Отсюда: (х-1)∙6-у∙(-3)+z∙2=0,
или 6х+3у+2z-6=0.
Площадь треугольника АВС найдем с
помощью векторного произведения
векторов AB и AC

Координаты вектора AB =(-1;2;0),
вектора AC =(-1,0,3).
1
SΔABC= AB AC
кв.единиц.
2
Векторное произведение:
i
j k
AB AC 1 2 0 6i 3 j 2k
1 0 3

Тогда
1
S ABC 6i 3 j 2k
2
1
7
36 9 4 3,5 êâ.åä.
2
2

Уравнение высоты - уравнение прямой по
точке D(2,3,4) и направляющему вектору. В
качестве направляющего вектора –
нормальный вектор грани АВС: n (6,3,2)
x 2 y 3 z 4
6
3
2
Для нахождения длины высоты используем
формулу:
Ax0 By 0 Cz0 D
d
A2 B 2 C 2

Получим:
d
6 2 3 3 2 4 6
36 9 4
27
3
4. Угол между ребром AD и гранью АВС.
Уравнение грани АВС: 6х+3у+2z-6=0,
нормальный вектор имеет координаты:
(6,3,2). Напишем уравнения прямой,
проходящей через точки А(1,0,0) и D(2,3,4):
x 1 y 0 z 0
2 1 3 0 4 0

Эта прямая имеет направляющий вектор с
координатами:(1,3,4). Тогда
sin
=
Am Bn Cp
m n p A B C
2
2
2
2
6 1 3 3 2 4
12 32 4 2 6 2 32 2 2
arcsin
2
23
7 26
2
=
23
23
26 7 7 26

5. Объем пирамиды равен 1/6 объема
параллелепипеда, построенного на
векторах, как на сторонах. Используем
смешанное произведение векторов.
Координаты векторов: AB =(-1,2,0),
AC○ =(-1,0,3), AD =(1,3,4)
○ Vпараллелепипеда
1 2 0
1 0 3 23
1
3 4
○ Vпирамиды=23/6 куб.ед.

Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.

Пусть дана точка и направляющий вектор . Произвольная точка лежит на прямой l только в том случае, если векторы и коллинеарны, т. е. для них выполняется условие:

.

Приведённые выше уравнения и есть канонические уравнения прямой.

Числа m , n и p являются проекциями направляющего вектора на координатные оси. Так как вектор ненулевой, то все числа m , n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю. В аналитической геометрии допускается, например, такая запись:

,

которая означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz , т. е. плоскости yOz .

Пример 1. Составить уравнения прямой в пространстве, перпендикулярной плоскости и проходящей через точку пересечения этой плоскости с осью Oz .

Решение. Найдём точку пересечения данной плоскости с осью Oz . Так как любая точка, лежащая на оси Oz , имеет координаты , то, полагая в заданном уравнении плоскости x = y = 0 , получим 4z - 8 = 0 или z = 2 . Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2) . Поскольку искомая прямая перпендикулярна плоскости, она параллельна вектору её нормали . Поэтому направляющим вектором прямой может служить вектор нормали заданной плоскости.

Теперь запишем искомые уравнения прямой, проходящей через точку A = (0; 0; 2) в направлении вектора :

Уравнения прямой, проходящей через две данные точки

Прямая может быть задана двумя лежащими на ней точками и В этом случае направляющим вектором прямой может служить вектор . Тогда канонические уравнения прямой примут вид

.

Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.

Пример 2. Составить уравнение прямой в пространстве, проходящей через точки и .

Решение. Запишем искомые уравнения прямой в виде, приведённом выше в теоретической справке:

.

Так как , то искомая прямая перпендикулярна оси Oy .

Прямая как линия пересечения плоскостей

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и , т. е. как множество точек, удовлетворяющих системе двух линейных уравнений

Уравнения системы называются также общими уравнениями прямой в пространстве.

Пример 3. Составить канонические уравнения прямой в пространстве, заданной общими уравнениями

Решение. Чтобы написать канонические уравнения прямой или, что то же самое, уравнения прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например yOz и xOz .

Точка пересечения прямой с плоскостью yOz имеет абсциссу x = 0 . Поэтому, полагая в данной системе уравнений x = 0 , получим систему с двумя переменными:

Её решение y = 2 , z = 6 вместе с x = 0 определяет точку A (0; 2; 6) искомой прямой. Полагая затем в заданной системе уравнений y = 0 , получим систему

Её решение x = -2 , z = 0 вместе с y = 0 определяет точку B (-2; 0; 0) пересечения прямой с плоскостью xOz .

Теперь запишем уравнения прямой, проходящей через точки A (0; 2; 6) и B (-2; 0; 0) :

,

или после деления знаменателей на -2:

,

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

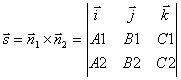Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Графический метод. Координатная плоскость (x;y)

Уравнения с параметром вызывают серьезные трудности логического характера. Каждое такое уравнение - это, по существу, краткая запись семейства уравнений. Ясно, что выписать каждое уравнение из бесконечного семейства невозможно, но, тем не менее, каждое из них должно быть решено. Легче всего это сделать с помощью графического представления зависимости переменной от параметра.

На плоскости функция задает семейство кривых зависящих от параметра. Нас будет интересовать с помощью какого преобразования плоскости можно переходить к другим кривым семейства (см. , , , , , , ).

Параллельный перенос

Пример . Для каждого значения параметра определить число решений уравнения.

Решение . Построим график функции.

Рассмотрим. Это прямая параллельна оси ОХ.

Ответ . Если, то решений нет;

если, то 3 решения;

если, то 2 решения;

если, 4 решения.

Поворот

Сразу следует отметить, что выбор семейства кривых не отличается однообразием (в отличие от самих задач), а точнее он один: во всех задачах - прямые. Более того, центр поворота принадлежит прямой.

Пример . При каких значениях параметра уравнение имеет единственное решение?

Решение . Рассмотрим функцию и. График второй функции - это полуокружность с центром в точке с координатами и радиусом =1 (рис. 2).

Дуга АВ.

Все лучи проходящие между ОА и ОВ пересекаются в одной точке, также в одной точке пересекаются ОВ и ОМ (касательная). Угловые коофициэнты ОА и ОВ равны соответственно. Угловой коэффициент касательной равен. Легко находится из системы

Итак, прямые семейства имеют с дугой только одну общую точку при.

Ответ . .

Пример . При каких уравнение имеет решение?

Решение . Рассмотрим функцию. Исследуя ее на монотонность узнаем, что она возрастает на промежутке и убывает на. Точка - является точкой максимума.

Функция же - это семейство прямых, проходящих через точку. Обратимся к рисунку 2. Графиком функции является дуга АВ. Прямые, которые будут находиться между прямыми ОА и ОВ, удовлетворяют условию задачи. Коэффициент наклона прямой ОА является число, а ОВ -- .

Ответ . При уравнение имеет 1 решение;

при остальных значениях параметра решений нет.

Гомотетия. Сжатие к прямой

Пример . Найти все значения параметра, при каждом из которых уравнение имеет ровно 8 решений.

Решение . Имеем. Рассмотрим функцию. Первая из них задает семейство полуокружностей с центром в точке с координатами, второе семейство прямых параллельных оси абсцисс.

Число корней будет соответствовать числу 8 тогда, когда радиус полуокружности будет больше и меньше, то есть. Заметим, что есть.

Ответ . или.

Графический метод. Координатная плоскость (x;a)

Вообще, уравнения , содержащие параметр, не обеспечены какой-либо четкой, методически оформленной системой решения. Те или иные значения параметра приходится искать на ощупь, перебором, решая большое количество промежуточных уравнений. Такой подход далеко не всегда обеспечивает успех в отыскании всех значений параметра, при которых уравнение не имеет решений, имеет одно, два и более решений. Зачастую часть значений параметра теряются или появляются лишние значения. Для того чтобы эти последние, приходится проводить специальное исследование которое может оказаться довольно трудным.

Рассмотрим метод, упрощающий работу по решению уравнений с параметром. Метод состоит в следующем

1. Из уравнения с переменной x и параметра a выразим параметр как функцию от x : .

2. В координатной плоскости x Oa строим график функции.

3. Рассмотрим прямые и выделим те промежутки оси Oa , на которых эти прямые удовлетворяют следующим условиям: a) не пересекает график функции, б) пересекает график функции в одной точке, в) в двух точках, г) в трех точках и так далее.

4. Если поставлена задача найти значения x , то выражаем x через a для каждого из найденных промежутков значения a в отдельности.

Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. Таким образом, возникает координатная плоскость. Казалось бы, такая незначительная деталь, как отказ от традиционного обозначения координатной плоскости буквами x и y определяет один из эффективнейших методов решения задач с параметрами.

Описанный метод очень нагляден. Кроме того, в нем находят применение почти все основные понятия курса алгебры и начал анализа. Задействуется весь набор знаний, связанных с исследованием функции: применение производной к определению точек экстремума, нахождение предела функции, асимптот и т . д. (см. , , ).

Пример . При каких значениях параметра уравнение имеет два корня?

Решение . Переходим к равносильной системе

Из графика видно, что при уравнение имеет 2 корня.

Ответ . При уравнение имеет два корня.

Пример . Найдите множество всех чисел, для каждого из которых уравнение имеет только два различных корня.

Решение . Перепишем данное уравнение в следующем виде:

Теперь важно не упустить, что, и - корни исходного уравнения лишь при условии. Обратим внимание на то, что график удобнее строить на координатной плоскости. На рисунке 5 искомый график - объединение сплошных линий. Здесь ответ «считывается» вертикальными прямыми.

Ответ . При, или, или.