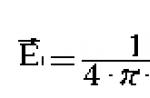Je-li elektrické pole vytvořeno jednobodovým nábojem q, pak intenzita tohoto pole v určitém bodě, který se nachází ve vzdálenosti r z poplatku je podle Coulombova zákona:
a směřuje podél přímky spojující náboj s tímto bodem. Síla pole bodového náboje se tedy mění, když se vzdaluje od náboje v nepřímé úměrnosti ke druhé mocnině vzdálenosti. S kladným nábojem q pole je nasměrováno podél poloměru od náboje, se záporem q– po poloměru směrem k náboji. Podívejme se, čemu je rovna intenzita pole způsobená dvěma bodovými náboji q 1 A q2. Nechat E 1- síla pole v určitém okamžiku A, způsobené nábojem q 1(při nabíjení q2 odstraněn) a E 2 je napětí ve stejném bodě způsobené nábojem q2(když je náboj odstraněn q 1). Tyto hodnoty jsou určeny vzorcem:
Zkušenosti ukazují, že při kombinovaném působení obou nábojů je intenzita pole v bodě A lze nalézt podle pravidla rovnoběžníku:
pokud z bodu A vyčlenit segmenty znázorňující modulo a ve směru tahu E 1 A E 2 , a na těchto segmentech, jako na stranách postavit rovnoběžník, pak napětí E výsledného pole v modulu a směru bude reprezentováno úhlopříčkou tohoto rovnoběžníku .
Pravidlo pro sčítání sil pole je podobné pravidlu pro sčítání sil v mechanice. Stejně jako v mechanice platí, že platnost paralelogramového pravidla znamená nezávislost na působení elektrických polí. Postupnou aplikací pravidla rovnoběžníku je možné vypočítat intenzitu pole nejen dvou. Ale také libovolný počet bodových poplatků.
Intenzita pole soustavy nábojů v daném bodě se rovná geometrickému (vektorovému) součtu sil pole vytvořených v tomto bodě každým nábojem zvlášť:
Toto tvrzení se nazývá princip superpozice elektrostatických polí.
referenční informace:
Napínací čáry - čáry, tečny, ke kterým se v každém bodě pole shoduje vektor intenzity elektrostatického pole v tomto bodě.
Linie napětí se neprotínají.
Kladný náboj je zdrojem čar napětí; záporný náboj je odvod napínacích čar.
Modul intenzity vektoru je úměrný stupni zesílení siločar elektrostatického pole. Elektrické pole, jehož vektory intenzity jsou ve všech bodech prostoru stejné, se nazývá homogenní.
Toto ustanovení platí v řadě případů. To je jeden z obecných fyzikálních zákonů, na kterých je fyzika jako věda postavena. To je to, co je pozoruhodné pro vědce, kteří jej používají v různých situacích.
Pokud vezmeme v úvahu princip superpozice v nejobecnějším smyslu, pak podle něj bude součet vlivu vnějších sil působících na částici součtem jednotlivých hodnot každé z nich.
Tento princip platí pro různé lineární systémy, tzn. systémy, jejichž chování lze popsat lineárními vztahy. Příkladem je jednoduchá situace, kdy se lineární vlna šíří v nějakém konkrétním prostředí, přičemž její vlastnosti zůstanou zachovány i pod vlivem poruch vznikajících samotnou vlnou. Tyto vlastnosti jsou definovány jako konkrétní součet účinků každé z harmonických složek.
Aplikace
Jak již bylo zmíněno, princip superpozice má poměrně široké uplatnění. Jeho působení lze nejzřetelněji vidět v elektrodynamice. Je však důležité mít na paměti, že s ohledem na princip superpozice to fyzika nepovažuje za konkrétní postulát, konkrétně za důsledek teorie elektrodynamiky.
Například v elektrostatice tento princip funguje při studiu, systém nábojů v určitém bodě vytváří napětí, které bude součtem sil pole každého z nábojů. Tento závěr se využívá v praxi, protože jej lze použít k výpočtu potenciální energie elektrostatické interakce. V tomto případě bude nutné vypočítat potenciální energii každého jednotlivého náboje.
To podporuje Maxwellova rovnice, která je ve vakuu lineární. Z toho také vyplývá, že světlo se nerozptyluje, ale šíří se lineárně, takže jednotlivé paprsky spolu neinteragují. Ve fyzice se tento jev často nazývá princip superpozice v optice.
Je třeba také poznamenat, že v klasické fyzice princip superpozice vyplývá z linearity rovnic jednotlivých pohyblivých lineárních systémů, a proto je přibližný. Je založeno na hlubokých dynamických principech, ale blízkost z něj nečiní ani univerzální, ani zásadní.
Zejména silný je popsán jinými rovnicemi, nelineárními, a proto princip nelze v těchto situacích aplikovat. Makroskopický se také neřídí tímto principem, protože závisí na vlivu vnějších polí.
Princip superpozice sil je však v kvantové fyzice zásadní. Pokud se v jiných sekcích používá s nějakými chybami, tak na kvantové úrovni funguje celkem přesně. Jakýkoli kvantově mechanický systém je zobrazován z a vektorů lineárního prostoru, a pokud se podřizuje lineárním funkcím, pak je jeho stav určen principem superpozice, tzn. je superpozice každého stavu a vlnové funkce.
Hranice použití jsou spíše libovolné. Rovnice klasické elektrodynamiky jsou lineární, ale to není hlavní pravidlo. Většina základních teorií fyziky je založena na nelineárních rovnicích. To znamená, že v nich nebude naplněn princip superpozice, sem můžeme zařadit obecnou teorii relativity, kvantovou chromodynamiku a také Yang-Millsovu teorii.
V některých systémech, kde jsou principy linearity použitelné jen částečně, lze podmíněně uplatnit i princip superpozice, například slabé gravitační interakce. Navíc při zvažování interakce atomů a molekul také není zachován princip superpozice, což vysvětluje rozmanitost fyzikálních a chemických vlastností materiálů.
Tělesa s určitým objemem a lineárními rozměry vždy zabírají část prostoru, ve kterém se nemohou nacházet jiná tělesa, aniž by se změnily určité charakteristiky. Kde je kámen, nemůže být ani jiný kámen, ani kovová koule, ani žádný jiný hmotný předmět.
Charakteristickým rysem elektrického pole je, že na rozdíl od látky mohou být pole různých zdrojů a různého původu současně umístěna v jednom bodě prostoru. Každý obor si přitom zachovává svou individualitu a žádná z jeho charakteristik se nemění pod vlivem jiného oboru. Jedním z potvrzení toho je známý příklad šíření rádiových vln, které jsou proměnným elektromagnetickým polem. Rádiová vlna šířící se ze severu na jih vůbec neovlivňuje vlnu, která se šíří ze západu na východ. A posluchač, přijímající informace, které přinesla první vlna, si ani neuvědomuje, že se tato vlna „setkala“ s jinou.
To je také pozorováno v případě, kdy existuje určitý systém nabitých těles a jim odpovídajících polí.
Nechť se v nějakém bodě prostoru A nachází těleso s kladným nábojem Q1(obr. 4.33). Zavedeme-li do libovolného bodu B bodové těleso s kladným nábojem q 0, pak na něj bude působit síla F 1 jako výsledek interakce tělesa B s polem tělesa A.
V libovolném bodě C zavedeme těleso s nábojem Q2(obr. 4.34). Jeho pole bude působit na těleso B silou F 2.Žádná změna hodnoty síly F 1 se nestane. Z mechaniky je ale známo, že působí-li na těleso více sil, pak je lze nahradit výslednicí (obr. 4.35).
V případě více zdrojů elektrického pole
F =F 1+F 2 + … + Fn.
Pokud je levá a pravá strana rovnice dělena q 0, pak dostaneme
F̅ /q 0 =F 1 / q0 + F 2 / q0 + … + Fn/q 0,
E = E̅ 1 + E̅ 2 + … + E̅n.
Proto při výpočtu interakce nabitého tělesa s elektrickými poli z různých zdrojů lze použít koncept síly „celkového“ elektrického pole. Tento závěr je formulován jako princip superpozice.materiál z webu
Princip superpozice over-ley. Síla elektrického pole soustavy nabitých těles v libovolném bodě je rovna vektorovému součtu sil polí jednotlivých těles v daném bodě.
V matematické podobě je tento princip zapsán takto:
E = E̅ 1 + E̅ 2 + … + En
Kde E̅ - síla pole soustavy nabitých těles; E̅ 1,E 2…- intenzita polí každého z těles, která jsou součástí systému.
Síla elektrického pole tělesa, které má stejný počet kladně a záporně nabitých částic, je nulová.
Princip superpozice nad-lei není omezeno počtem těles v systému. Proto je intenzita elektrického pole nenabitého tělesa, které zahrnuje obrovské množství částic s kladným i záporným nábojem, prakticky nulová.
Na této stránce jsou materiály k tématům:
Jak je formulován princip superpozice polí
Vzorec principu superpozice sil
Princip superpozice elektrických polí stručně
Vzorec principu superpozice
Jaký výraz je matematický zápis principu superpozice polí?
Otázky k této položce:
Jedním z hlavních úkolů elektrostatiky je odhadnout parametry pole pro dané, stacionární, rozložení nábojů v prostoru. Jeden ze způsobů řešení takových problémů je založen na princip superpozice . Jeho podstata je následující.
Je-li pole tvořeno několika bodovými náboji, pak je zkušební náboj q ovlivněn nábojem qk, jako by žádné jiné náboje nebyly. Výsledná síla je určena výrazem:
Protože , pak je také výsledná intenzita pole v bodě, kde se nachází zkušební náboj dodržuje princip superpozice :
 |
(1.4.1) |
Tento poměr vyjadřuje princip superpozice resp superpozice elektrických polí a představuje důležitou vlastnost elektrického pole. Intenzita výsledného pole soustavy bodových nábojů je rovna vektorovému součtu sil polí vytvořených v daném bodě každým z nich samostatně.
Zvažte použití principu superpozice v případě pole vytvořeného elektrickým systémem dvou nábojů se vzdáleností mezi náboji rovnou l(obr. 1.2).
Rýže. 1.2
Pole vytvořená různými náboji se navzájem neovlivňují, takže vektor výsledného pole několika nábojů lze zjistit pravidlem sčítání vektorů (pravidlo paralelogramu)
 .
|
V tomto případě
A 
Proto,
 |
(1.4.2) |
Podívejme se na další příklad. Najděte sílu elektrostatického pole E vytvořené dvěma kladnými náboji q 1 A q2 na místě A umístěné na dálku r1 od prvního a r2 z druhého náboje (obr. 1.3).
Rýže. 1.3
Použijeme kosinovou větu:
| (1.4.3) |
Kde 
.
Pokud je pole vytvořeno ne bodové poplatky, pak se v takových případech používá obvyklá technika. Tělo je rozděleno do nekonečně malých prvků a je určena intenzita pole generovaná každým prvkem, poté integrována do celého těla:
| (1.4.4) |
Kde je síla pole způsobená nabitým prvkem. Integrál může být lineární, plošný nebo objemový, v závislosti na tvaru tělesa. K vyřešení těchto problémů použijte odpovídající hodnoty hustoty náboje:
– hustota lineárního náboje, měřená v C/m;
je hustota povrchového náboje, měřená v C/m2;
je objemová hustota náboje, měřená v C/m3.
Pokud je pole tvořeno nabitými tělesy složitého tvaru a nerovnoměrně nabitými, pak pomocí principu superpozice je obtížné výsledné pole najít.
vzorec (1.4.4) vidíme, že je to vektorová veličina:
 |
(1.4.5) |
Integrace tedy může být složitá. K výpočtu se proto často používají jiné metody, kterým se budeme věnovat v následujících tématech. V některých relativně jednoduchých případech však tyto vzorce umožňují analyticky vypočítat .
Jako příklady zvažte lineární rozložení náboje nebo kruhové rozložení náboje.
Určíme sílu elektrického pole v bodě A(obr. 1.4) ve vzdálenosti x od nekonečně dlouhého, lineárního, rovnoměrně rozloženého náboje. Nechť λ je náboj na jednotku délky.
Rýže. 1.4
Předpokládáme, že x je malé ve srovnání s délkou vodiče. Zvolme souřadnicový systém tak, aby se osa y shodovala s vodičem. Délkový prvek dy, nese náboj Síla elektrického pole vytvořená tímto prvkem v bodě A.
| , |
kde = je vektor shodný ve směru s normálou k povrchu (jednotkový vektor normály k povrchu) a modulo se rovná ploše . Protože integrál je skalárním součinem vektorů, tok může být buď kladný nebo záporný, v závislosti na volbě směru vektoru. Geometricky je proudění úměrné počtu siločar pronikající danou oblastí (viz obr. 2.3.1).
Gaussova věta.
Tok vektoru síly elektrického pole libovolným
uzavřená plocha se rovná algebraickému součtu nábojů v ní
uvnitř tohoto povrchu, rozdělený(v soustavě SI)
| . (2.3.1) |
V případě uzavřené plochy se vektor volí od plochy směrem ven.
Pokud tedy siločáry opustí povrch, tok bude pozitivní, a pokud vstoupí, bude negativní.
Výpočet elektrických polí pomocí Gaussovy věty.
V řadě případů se počítá síla elektrického pole podle Gaussovy věty
ukazuje se to docela jednoduše. Je však založen na principu superpozice.
Protože pole bodového náboje je středově symetrické, pole
centrálně symetrického systému poplatků bude také středově symetrický. Nejjednodušším příkladem je pole rovnoměrně nabité koule. Pokud má rozložení náboje osovou symetrii, pak se struktura pole bude také lišit v osové symetrii. Příkladem je nekonečný rovnoměrně nabitý závit nebo válec. Pokud je náboj rovnoměrně rozložen v nekonečné rovině, pak siločáry budou symetrické podle symetrie náboje. Tento způsob výpočtu se tedy používá v případě vysokého stupně symetrie rozložení náboje, který vytváří pole. Dále uvedeme příklady výpočtu takových polí.
Elektrické pole rovnoměrně nabité koule.
Koule o poloměru je rovnoměrně nabitá objemovou hustotou. Pojďme spočítat pole uvnitř míče.
Systém nabíjení je centrálně symetrický. V
jako integrační plochu, kterou zvolíme
poloměr koule r(r<R), jehož střed se shoduje
se středem symetrie náboje (viz obr.2.3.2). Vypočítejme vektorový tok touto plochou.
Vektor směřuje podél poloměru. Od pole
má tedy středovou symetrii
význam E bude ve všech bodech stejný
vybraný povrch. Pak
Nyní najdeme náboj uzavřený uvnitř vybraného povrchu
Všimněte si, že pokud je náboj rozložen ne po celém objemu koule, ale pouze po jejím povrchu (nabitý koule), pak bude síla pole uvnitř nula.
Pojďme spočítat pole mimo míč viz obr. 2.3.3.
Nyní integrační plocha zcela pokrývá celou náplň kuličky. Gaussovu větu lze zapsat ve tvaru
Bereme v úvahu, že pole je středově symetrické
Nakonec pro intenzitu pole mimo nabitou kouli získáme
Pole mimo rovnoměrně nabitou kouli tedy bude mít stejný tvar jako u bodového náboje umístěného ve středu koule. Stejný výsledek dostaneme pro rovnoměrně nabitou kouli.
Výsledek (2.3.2) a (2.3.3) můžete analyzovat pomocí grafu na obr.2.3.4.
Elektrické pole nekonečného rovnoměrně nabitého válce.
Nechť je nekonečně dlouhý válec rovnoměrně nabitý objemovou hmotností.
Poloměr válce je . Najdeme pole uvnitř válce, jako funkci
osová vzdálenost. Protože systém nábojů má osovou symetrii,
integrační plochu také mentálně volíme válec menší
poloměr a libovolná výška , jejichž osa se shoduje s osou symetrie problému (obr.2.3.5). Vypočítejme průtok povrchem tohoto válce a rozdělíme ho na integrál přes povrch pláště
nost a na základě
Z důvodů symetrie
z toho vyplývá, že směřuje radiálně. Potom, protože siločáry nepronikají žádnou ze základen zvoleného válce, je průtok těmito plochami nulový. Vektorový tok bočním povrchem válce bude zapsán:
Oba výrazy dosadíme do původního vzorce Gaussovy věty (2.3.1)
Po jednoduchých transformacích získáme výraz pro intenzitu elektrického pole uvnitř válce
I v tomto případě, pokud je náboj rozložen pouze po povrchu válce, je intenzita pole uvnitř nulová.
Nyní najdeme pole mimo nabitý válec
V duchu si zvolíme jako plochu, kterou budeme tok vektoru počítat, válec o poloměru a libovolné výšce (viz obr. 2.3.6).
Proud bude zaznamenáván stejným způsobem jako pro vnitřní oblast. A náboj uzavřený uvnitř mentálního válce se bude rovnat:
Po jednoduchých transformacích získáme výraz pro sílu elektrického
pole mimo nabitý válec:
Zavedeme-li v této úloze lineární hustotu náboje, tzn. náboj na jednotku délky válce , pak se výraz (2.3.5) převede do tvaru
Což odpovídá výsledku získanému pomocí principu superpozice (2.2.14).
Jak vidíme, závislosti ve výrazech (2.3.4) a (2.3.5) jsou různé. Pojďme sestavit graf.
Pole nekonečné rovnoměrně nabité roviny .
Nekonečná rovina je rovnoměrně nabitá povrchovou hustotou. Siločáry elektrického pole jsou symetrické kolem této roviny, a proto je vektor kolmý k nabité rovině. V duchu si vybereme válec libovolných velikostí pro integraci a umístíme jej podle obr. 2.3.8. Napíšeme Gaussovu větu :) může být pohodlné zavést skalární charakteristický změny pole, nazývané divergence. Pro určení této charakteristiky zvolíme malý objem v poli poblíž určitého bodu R a najděte vektorový tok povrchem ohraničujícím tento objem. Poté získanou hodnotu vydělíme objemem a vezmeme mez výsledného poměru, když se objem smrští do daného bodu R. Výsledná hodnota se nazývá vektorová divergence
. (2.3.7)
Vyplývá to z toho, co bylo řečeno. (2.3.8)
Tento poměr se nazývá Gaussova-Ostrogradského věta, platí pro libovolné vektorové pole.
Poté z (2.3.1) a (2.3.8), přičemž se bere v úvahu, že náboj obsažený v objemu PROTI, můžeme napsat, že dostaneme
nebo, protože v obou částech rovnice je integrál převzat stejný objem,
Tato rovnice matematicky vyjadřuje Gaussova věta pro elektrické pole v diferenciálním tvaru.
Význam operace divergence spočívá v tom, že zjišťuje přítomnost zdrojů pole (zdrojů siločar). Body, kde divergence není rovna nule, jsou zdroji siločar. Siločáry elektrostatického pole tedy začínají a končí u nábojů.
