1 arc de definire a cercului unui unghi central de cerc. Tot ce trebuie să știi despre cerc

Lasă
- punctul arbitrar al elipsei. Avem:
,
. Din definiția unei elipse

, (1.29)

sau - ecuația necesară a elipsei, care este incomod de utilizat. Din ultima egalitate rezultă că .De vreme ce
, atunci putem pătra ambele părți ale ecuației și după transformări echivalente obținem:
. Prin urmare,. Să introducem o nouă variabilă
. Avem:
. Din această egalitate rezultă că

. (1.30)

Ecuația (1.30) se numește ecuația canonică (cea mai simplă) a elipsei. Această ecuație este o ecuație de ordinul doi. Astfel, orice punct al elipsei care satisface ecuația (1.29) satisface și ecuația (1.30). Să demonstrăm că toate punctele planului ale căror coordonate satisfac ecuația (1.30) sunt puncte ale unei elipse, adică coordonatele lor satisfac ecuația (1.29).

Pentru raza focală relatia tine
. Din ecuația (1.30) avem:
. De aceea
, sau
. În mod similar, găsim că
. Prin urmare,
.

Elipsa este simetrică față de axele de coordonate, deoarece conține doar puteri pare Şi , și relativ la origine. Axele de simetrie ale unei elipse se numesc axe ale ei, iar centrul de simetrie este centrul elipsei.

Elipsa intersectează axele de coordonate în puncte
,
,
,
. Aceste puncte sunt numite vârfuri ale elipsei. La
elipsa degenerează într-un cerc cu rază și centru la origine. Vârfurile elipsei limitează segmentele de lungime pe axe
Şi
, și
(acest lucru rezultă din faptul că
).

Cantitati Şi sunt numite semiaxele majore și minore ale elipsei, axele elipsei sunt axa majoră și, respectiv, minoră.

Definiţie. Excentricitatea elipsei se numeste relatie unde - jumătate din distanța dintre focalizări, - semiaxa mare, i.e.

. (1.31)

Având în vedere că
, primim
. Deoarece

, Asta
. Dacă
, adică elipsa se apropie de un cerc, atunci
. Dacă
, A nu tinde spre zero, atunci elipsa este alungită de-a lungul axei majore. Astfel, excentricitatea unei elipse caracterizează măsura alungirii acesteia de-a lungul axei majore.

Dacă focarele elipsei
Şi
situat pe axa ordonatelor, apoi în acest caz
iar cel mare este arborele axului . Ecuația elipsei are și forma (1.30), dar
, iar excentricitatea sa este calculată prin formula
.

Exemplul 14. Scrieți o ecuație pentru o elipsă ale cărei focare se află pe axa x simetric față de origine, știind că distanța dintre focarele sale
și excentricitatea
.

Soluţie. Jumătate din distanța dintre focalizări
. Focarele elipsei sunt situate pe axa x, deci semiaxa majoră este . Din (1.31) rezultă că
. Apoi. Astfel, ecuația elipsei are forma
.

Exemplul 15. Dată o elipsă
. Găsiți-i semiaxele, focarele, excentricitatea.

Soluţie. Să reducem ecuația elipsei la formă canonică. Pentru a face acest lucru, împărțim ambele părți ale ecuației la 45, obținem
. Astfel, semiaxa sa
,
. Semiaxa majoră este semiaxa , prin urmare focarele elipsei sunt situate pe axa ordonatelor și

, prin urmare, focarele sunt în puncte
Şi
. Excentricitatea elipsei este egală cu raportul dintre jumătatea distanței dintre focare și semiaxa majoră, adică.
.

Exemplul 16. Calculați aria unui patrulater
, două vârfuri Şi care se află la focarele elipsei
, încă doi Şi
coincide cu capetele axei sale minore.

Soluţie. Ecuația canonică a elipsei are forma
, De aceea
,
. Prin urmare, vârfurile patrulaterului Şi
au coordonatele corespunzătoare
Şi
. Să găsim coordonatele vârfurilor Şi . Deoarece
, Asta
,
. Patrulaterul rezultat este simetric față de axele de coordonate și față de originea coordonatelor , prin urmare,

.

ŞI cerc- forme geometrice interconectate. există o linie întreruptă de graniță (curbă) cerc,

Definiţie. Un cerc este o curbă închisă, fiecare punct fiind echidistant de un punct numit centrul cercului.

Pentru a construi un cerc, se selectează un punct arbitrar O, luat ca centru al cercului, și se trasează o linie închisă folosind o busolă.

Dacă punctul O al centrului cercului este conectat la puncte arbitrare ale cercului, atunci toate segmentele rezultate vor fi egale între ele, iar astfel de segmente se numesc raze, prescurtate cu litera latină mică sau majusculă „er” ( r sau R). Puteți desena atâtea raze într-un cerc câte puncte există în circumferință.

Un segment care leagă două puncte dintr-un cerc și care trece prin centrul său se numește diametru. Diametru constă din două razele, întins pe aceeași linie dreaptă. Diametrul este indicat prin litera latină mică sau majusculă „de” ( d sau D).

Regulă. Diametru un cerc este egal cu două dintre ele razele.

d = 2r
D=2R

Circumferința unui cerc este calculată prin formula și depinde de raza (diametrul) cercului. Formula conține numărul ¶, care arată de câte ori circumferința este mai mare decât diametrul său. Numărul ¶ are un număr infinit de zecimale. Pentru calcule s-a luat ¶ = ​​3,14.

Circumferința unui cerc este notă cu litera majusculă latină „tse” ( C). Circumferința unui cerc este proporțională cu diametrul acestuia. Formule pentru calcularea circumferinței unui cerc pe baza razei și diametrului acestuia:

C = ¶d
C = 2¶r

• Exemple
• Dat: d = 100 cm.
• Circumferinta: C=3,14*100cm=314cm
• Dat: d = 25 mm.
• Circumferinta: C = 2 * 3,14 * 25 = 157mm

Secanta circulară și arc de cerc

Fiecare secantă (linie dreaptă) intersectează un cerc în două puncte și îl împarte în două arce. Mărimea arcului de cerc depinde de distanța dintre centru și secantă și se măsoară de-a lungul unei curbe închise de la primul punct de intersecție al secantei cu cerc până la al doilea.

Arcuri cercurile sunt împărțite secantăîntr-o majoră și una minoră dacă secanta nu coincide cu diametrul și în două arce egale dacă secanta trece de-a lungul diametrului cercului.

Dacă o secanta trece prin centrul unui cerc, atunci segmentul ei situat între punctele de intersecție cu cerc este diametrul cercului sau cea mai mare coardă a cercului.

Cu cât secanta este situată mai departe de centrul cercului, cu atât este mai mică măsura gradului arcului mai mic al cercului și mai mare este arcul mai mare al cercului, iar segmentul secantei, numit coardă, scade pe măsură ce secanta se îndepărtează de centrul cercului.

Definiţie. Un cerc este o parte a unui plan situat în interiorul unui cerc.

Centrul, raza și diametrul unui cerc sunt simultan centrul, raza și diametrul cercului corespunzător.

Deoarece un cerc face parte dintr-un plan, unul dintre parametrii acestuia este aria.

Regulă. Aria unui cerc ( S) este egal cu produsul pătratului razei ( r 2) la numărul ¶.

• Exemple
• Dat: r = 100 cm
• Zona cercului:
• S = 3,14 * 100 cm * 100 cm = 31.400 cm 2 ≈ 3 m 2
• Dat: d = 50 mm
• Zona cercului:
• S = ¼ * 3,14 * 50 mm * 50 mm = 1.963 mm 2 ≈ 20 cm 2

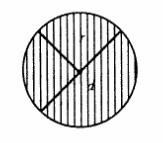
Dacă desenați două raze într-un cerc în puncte diferite ale cercului, atunci se formează două părți ale cercului, care se numesc sectoare. Dacă desenați o coardă într-un cerc, atunci se numește partea din plan dintre arc și coardă segment de cerc.

Definiția 2

Un poligon care satisface condiția definiției 1 se numește circumscris unui cerc.

Figura 1. Cerc înscris

Teorema 1 (despre un cerc înscris într-un triunghi)

Teorema 1

Puteți înscrie un cerc în orice triunghi și doar unul.

Dovada.

Luați în considerare triunghiul $ABC$. Să desenăm bisectoare în el care se intersectează în punctul $O$ și să tragem perpendiculare din el pe laturile triunghiului (Fig. 2)

Figura 2. Ilustrarea teoremei 1

Existență: Să desenăm un cerc cu centrul în punctul $O$ și raza $OK.\ $Deoarece punctul $O$ se află pe trei bisectoare, este echidistant de laturile triunghiului $ABC$. Adică $OM=OK=OL$. În consecință, cercul construit trece și prin punctele $M\ și\ L$. Deoarece $OM,OK\ și\ OL$ sunt perpendiculare pe laturile triunghiului, atunci după teorema tangentei cercului, cercul construit atinge toate cele trei laturi ale triunghiului. Prin urmare, din cauza arbitrarului unui triunghi, un cerc poate fi înscris în orice triunghi.

Unicitate: Să presupunem că un alt cerc cu centrul în punctul $O"$ poate fi înscris în triunghiul $ABC$. Centrul său este echidistant de laturile triunghiului și, prin urmare, coincide cu punctul $O$ și are o rază egală cu lungime $OK$ Dar atunci acest cerc va coincide cu primul.

Teorema a fost demonstrată.

Corolarul 1: Centrul unui cerc înscris într-un triunghi se află în punctul de intersecție al bisectoarelor sale.

Iată câteva fapte legate de conceptul de cerc înscris:

Nu orice patrulater poate încadra într-un cerc.

În orice patrulater circumscris, sumele laturilor opuse sunt egale.

Dacă sumele laturilor opuse ale unui patrulater convex sunt egale, atunci poate fi înscris un cerc în el.

Definiția 3

Dacă toate vârfurile unui poligon se află pe un cerc, atunci cercul se numește circumscris poligonului (Fig. 3).

Definiția 4

Un poligon care satisface definiția 2 se spune că este înscris într-un cerc.

Figura 3. Cerc circumscris

Teorema 2 (despre cercul circumferitor al unui triunghi)

Teorema 2

În jurul oricărui triunghi poți descrie un cerc și doar unul.

Dovada.

Luați în considerare triunghiul $ABC$. Să desenăm bisectoare perpendiculare în el, care se intersectează în punctul $O$ și să o conectăm cu vârfurile triunghiului (Fig. 4)

Figura 4. Ilustrarea teoremei 2

Existență: Să construim un cerc cu centrul în punctul $O$ și raza $OC$. Punctul $O$ este echidistant de vârfurile triunghiului, adică $OA=OB=OC$. În consecință, cercul construit trece prin toate vârfurile unui triunghi dat, ceea ce înseamnă că este circumscris acestui triunghi.

Unicitate: Să presupunem că un alt cerc poate fi descris în jurul triunghiului $ABC$ cu centrul său în punctul $O"$. Centrul său este echidistant de vârfurile triunghiului și, prin urmare, coincide cu punctul $O$ și are o rază egală cu lungimea $OC $ Dar atunci acest cerc va coincide cu primul.

Teorema a fost demonstrată.

Corolarul 1: Centrul cercului circumscris triunghiului coincide cu punctul de intersecție al perpendicularelor sale bisectoriale.

Iată câteva fapte legate de conceptul de cerc circumscripționar:

Nu este întotdeauna posibil să descrii un cerc în jurul unui patrulater.

În orice patrulater ciclic, suma unghiurilor opuse este $(180)^0$.

Dacă suma unghiurilor opuse ale unui patrulater este $(180)^0$, atunci se poate trasa un cerc în jurul lui.

Un exemplu de problemă privind conceptele de cercuri înscrise și circumscrise

Exemplul 1

ÎN triunghi isoscel baza este de 8 cm, latura este de 5 cm. Aflați raza cercului înscris.

Soluţie.

Luați în considerare triunghiul $ABC$. Prin corolarul 1, știm că centrul cercului se află la intersecția bisectoarelor. Să desenăm bisectoarele $AK$ și $BM$, care se intersectează în punctul $O$. Să desenăm o perpendiculară $OH$ din punctul $O$ pe latura $BC$. Să desenăm o poză:

Figura 5.

Deoarece triunghiul este isoscel, atunci $BM$ este atât mediana, cât și înălțimea. După teorema lui Pitagora $(BM)^2=(BC)^2-(MC)^2,\ BM=\sqrt((BC)^2-\frac((AC)^2)(4))=\ sqrt (25-16)=\sqrt(9)=$3. $OM=OH=r$ -- raza necesară a cercului înscris. Deoarece $MC$ și $CH$ sunt segmente de tangente care se intersectează, atunci după teorema tangentelor care se intersectează, avem $CH=MC=4\ cm$. Prin urmare, $BH=5-4=1\ cm$. $BO=3-r$. Din triunghiul $OHB$, conform teoremei lui Pitagora, obținem:

\[((3-r))^2=r^2+1\] \ \ \

Răspuns:$\frac(4)(3)$.

Circumferinţă este locul punctelor din plan echidistant de un punct fix numit centru.

Fie punctul să fie centrul și punctul
, este un punct arbitrar pe cerc. Apoi

unde se numeste R rază cerc sau extins

Ecuația (4) se numește canonic ecuația unui cerc.

Comentariu. Dacă în ecuația (4) notăm
,
și împărțiți ambele părți la
, obținem ecuația
. Că. un cerc este un caz special al unei elipse cu semi-axe egale.

7.1.3. Hiperbolă

Hiperbolă este locul geometric al punctelor din plan, pentru fiecare dintre care modulul diferenței de distanțe de la două puncte fixe, numit trucuri, este o valoare constantă.

Lasă
, - focalizări, distanță
,M este un punct arbitrar al hiperbolei. Apoi, conform definiției, avem

, (5)

Unde O– valoarea specificată.

Să introducem un sistem de coordonate folosind metoda prezentată mai jos în figură.

atunci relația (5) după transformări algebrice și eliminarea iraționalității poate fi reprezentată ca:

(6)

care se numeste ecuația canonică a unei hiperbole.În acest sistem de coordonate și în ecuația specificată (6), graficul hiperbolei are forma:

Dacă ecuația hiperbolei are forma

(7)

apoi, în consecință, graficul său arată astfel:

Opțiuni Şi numite semi-axe - valabil, - explicit. Parametru

(8)

numit excentricitate. Caracterizează forma unei hiperbole.

Să notăm câteva proprietăți ale unei hiperbole.

1) O hiperbolă are cel puțin două axe de simetrie și un centru de simetrie.

Într-adevăr, punct (0;0) pentru orice locație a graficului hiperbolei în sistemul de coordonate canonic, acesta este centrul de simetrie. Rolul axelor de simetrie este jucat de axele OHŞi Op-amp.

2) O hiperbolă intersectează una dintre axele de simetrie în două puncte numiteculmi , hiperbola nu se intersectează cu cealaltă axă de simetrie.

Astfel, în primul grafic, vârfurile hiperbolei (6) sunt situate pe axă OH, acestea sunt punctele
Şi
, pe al doilea grafic (7) - pe axă Op-amp,-Acest
Şi
.

3) O hiperbola are asimptote, adică linii drepte de care hiperbola se apropie fără limită., dacă un punct care alunecă de-a lungul lui merge la infinit.

Pentru o hiperbolă cu ecuație canonică
asimptotele sunt descrise prin ecuații

Şi
. (9)

Pentru o hiperbolă dată de ecuație
asimptotele sunt date prin linii drepte

. (10)

Trucuri hiperbole
(sau
Pentru
) sunt situate pe aceeași axă cu vârfurile sale. Aici

. (11)

Proprietatea optică a unei hiperbole. O rază care iese dintr-unul dintre focarele hiperbolei, după reflectarea sa din curbă, se deplasează ca și cum ar fi ieșit din al doilea focar.

7.1.4. Parabolă

Parabolă este locul punctelor din plan echidistant de un punct fix, numit se concentreze, și această linie, care se numește directoare.

Să fie drept l, - directoare, - focalizare și îndepărtat de la directoare la distanță p, și punct M, este un punct arbitrar al parabolei. Apoi

Să alegem un sistem de coordonate așa cum se arată mai jos.

.

Apoi, ecuația parabolei, după eliminarea iraționalității, va lua forma

,
(12)

care se numeste ecuația parabolă canonică. În acest sistem de coordonate și în ecuația specificată (12), graficul parabolei are forma:

Pentru ecuația parabolă canonică găsită, ecuația directrice

,
(13)

și concentrează-te situat la punct
.

Să notăm una dintre proprietăți.

O parabolă are o axă de simetrie.

În sistemul de coordonate ales mai sus, axa de simetrie a parabolei este OH.

Comentariu. 1. Dacă focalizarea are coordonate
, iar directriza este descrisă de ecuație
, atunci ecuația parabolei ia forma

. (14)

Dacă focalizarea este plasată pe axă 0y, atunci ecuația ia forma

sau
, (15)

în funcție de locația directoarei (
sau
, respectiv). Aceste ecuații sunt numite și canonic. Caracteristicile notate fac posibilă determinarea fără ambiguitate a locației parabolei și a trăsăturilor sale caracteristice (coordonatele focalizării, ecuația directricei).

Opticproprietateparabole. Razele paralele cu axa parabolei, după reflectarea din curbă, trec prin focarul acesteia.

În acest articol vom analiza în detaliu definiția cercului numeric, vom afla proprietatea sa principală și vom aranja numerele 1,2,3 etc. Despre cum să marcați alte numere pe cerc (de exemplu, \(\frac(π)(2), \frac(π)(3), \frac(7π)(4), 10π, -\frac(29π) ( 6)\)) înțelege .

Cercul numeric numit cerc cu raza unitară ale cărui puncte corespund , aranjate după următoarele reguli:

1) Originea este în punctul extrem drept al cercului;

2) În sens invers acelor de ceasornic - sens pozitiv; în sensul acelor de ceasornic – negativ;

3) Dacă trasăm distanța \(t\) pe cerc în direcția pozitivă, atunci vom ajunge la un punct cu valoarea \(t\);

4) Dacă trasăm distanța \(t\) pe cerc în direcția negativă, atunci vom ajunge la un punct cu valoarea \(–t\).

De ce se numește cercul cerc numeric?
Pentru că are numere pe el. În acest fel, cercul este similar cu axa numerelor - pe cerc, ca și pe axă, există un punct specific pentru fiecare număr.

De ce știi ce este un cerc numeric?
Folosind cercul numeric, se determină valorile sinusurilor, cosinusurilor, tangentelor și cotangentelor. Prin urmare, pentru a cunoaște trigonometria și a promova examenul de stat unificat cu peste 60 de puncte, trebuie să înțelegeți ce este un cerc numeric și cum să plasați puncte pe el.

Ce înseamnă cuvintele „...de raza unității...” în definiție?
Aceasta înseamnă că raza acestui cerc este egală cu \(1\). Și dacă construim un astfel de cerc cu centrul la origine, atunci se va intersecta cu axele în punctele \(1\) și \(-1\).

Nu trebuie să fie desenat mic; puteți modifica „dimensiunea” diviziunilor de-a lungul axelor, apoi imaginea va fi mai mare (vezi mai jos).

De ce raza este exact una? Acest lucru este mai convenabil, deoarece în acest caz, când se calculează circumferința folosind formula \(l=2πR\), obținem:

Lungimea cercului numeric este \(2π\) sau aproximativ \(6,28\).

Ce înseamnă „... ale căror puncte corespund numerelor reale”?
După cum am spus mai sus, pe cercul numeric pentru orice număr real va exista cu siguranță „locul” acestuia - un punct care corespunde acestui număr.

De ce să determinați originea și direcția pe cercul numeric?
Scopul principal al cercului numeric este de a determina în mod unic punctul său pentru fiecare număr. Dar cum puteți determina unde să puneți punctul dacă nu știți de unde să numărați și unde să vă mutați?

Aici este important să nu confundați originea pe linia de coordonate și pe cercul numeric - acestea sunt două sisteme de referință diferite! Și, de asemenea, nu confundați \(1\) pe axa \(x\) și \(0\) pe cerc - acestea sunt puncte pe diferite obiecte.

Care puncte corespund numerelor \(1\), \(2\), etc.?

Amintiți-vă, am presupus că cercul numeric are o rază de \(1\)? Acesta va fi segmentul nostru unitar (prin analogie cu axa numerelor), pe care îl vom reprezenta pe cerc.

Pentru a marca un punct pe cercul numeric corespunzător numărului 1, trebuie să mergeți de la 0 la o distanță egală cu raza în direcția pozitivă.

Pentru a marca un punct pe cerc corespunzător numărului \(2\), trebuie să parcurgeți o distanță egală cu două raze de la origine, astfel încât \(3\) să fie o distanță egală cu trei raze etc.

Când vă uitați la această imagine, este posibil să aveți 2 întrebări:
1. Ce se întâmplă când cercul „se termină” (adică facem o revoluție completă)?
Răspuns: să trecem la turul doi! Și când se termină al doilea, vom merge la al treilea și așa mai departe. Prin urmare, un număr infinit de numere poate fi trasat pe un cerc.

2. Unde vor fi numerele negative?
Răspuns: chiar acolo! Ele pot fi, de asemenea, aranjate, numărând de la zero numărul necesar de raze, dar acum în direcție negativă.

Din păcate, este dificil să notezi numere întregi pe cercul numeric. Acest lucru se datorează faptului că lungimea cercului numeric nu va fi egală cu un număr întreg: \(2π\). Și în locurile cele mai convenabile (în punctele de intersecție cu axele) vor exista și fracții, nu numere întregi